[题目]甲骑电动车从A地到B地.乙骑自行车从B地到A地.两人同时出发.设乙骑自行车的时间为t(h).两人之间的距离为s(km).图中的折线表示s和t之间的关系.根据图象回答下列问题．(1)A.B两地之间的距离为 km,(2)求甲出发多长时间与乙相遇? 题目和参考答案 ——青夏教育精英家教网—

【题目】甲骑电动车从A地到B地，乙骑自行车从B地到A地，两人同时出发，设乙骑自行车的时间为t（h），两人之间的距离为s（km），图中的折线表示s和t之间的关系，根据图象回答下列问题．

（1）A、B两地之间的距离为　　km；

（2）求甲出发多长时间与乙相遇？

参考答案：

【答案】（1）30；（2）甲出发h时与乙相遇．

【解析】

（1）直接从图上即可得到信息；

（2）先计算出甲乙的速度，再由题意得到试子30a+10a＝30，即可得到答案.

（1）由图象可得，

A、B两地之间的距离为30km，

故答案为：30；

（2）由图象可得，

甲的速度为30÷1＝30（km/h），乙的速度为：30÷3＝10（km/h），

设甲出发ah时与乙相遇，

30a+10a＝30，

解得，a＝，

答：甲出发h时与乙相遇．

相关试题

科目： 来源： 题型：

【题目】阅读理解：己知：对于实数a≥0，b≥0，满足a+b≥2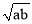，当且仅当a = b时，等号成立，此时取得代数式a+b的最小值．
根据以上结论，解决以下问题：
(1)拓展：若a>0，当且仅当a=___时，a+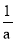有最小值，最小值为____；
(2)应用：
①如图1，已知点P为双曲线y=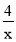(x>0)上的任意一点，过点P作PA⊥x轴，PB丄y轴，四边形OAPB的周长取得最小值时，求出点P的坐标以及周长最小值：
②如图2，已知点Q是双曲线y=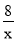(x>0)上一点，且PQ∥x轴，连接OP、OQ，当线段OP取得最小值时，在平面内取一点C，使得以0、P、Q、C为顶点的四边形是平行四边形，求出点C的坐标．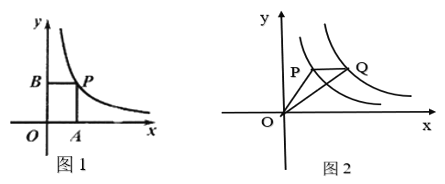
查看答案和解析>>
科目： 来源： 题型：

【题目】某校七年级有400名学生，其中2004年出生的有8人，2005年出生的有292人，2006年出生的有75人，其余的为2007年出生．
（1）该年级至少有两人同月同日生，这是一个　　事件（填“必然”、“不可能”或“随机”）；
（2）从这400名学生中随机选一人，选到2007年出生的概率是多少？
查看答案和解析>>
科目： 来源： 题型：

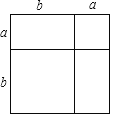
【题目】如图所示的大正方形是由两个小正方形和两个长方形组成．
（1）通过两种不同的方法计算大正方形的面积，可以得到一个数学等式；
（2）利用（1）中得到的结论，解决下面的问题：若a+b＝2，ab＝﹣3，
求：①a2+b2；
②a4+b4．
查看答案和解析>>
科目： 来源： 题型：

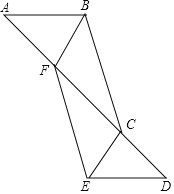
【题目】如图，在△ABC和△DEF中，AB∥DE，点A，F，C，D在同一直线上，AF＝CD，∠AFE＝∠BCD．
试说明：
（1）△ABC≌△DEF；
（2）BF∥EC．
查看答案和解析>>
科目： 来源： 题型：

【题目】问题背景：某数学兴趣小组把两个等腰直角三角形的直角顶点重合，发现了一些有趣的结论．
结论一：
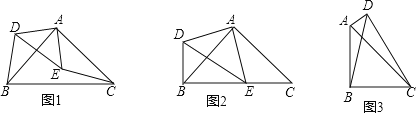
（1）如图1，在△ABC、△ADE中，∠BAC＝∠DAE＝90°，AB＝AC，AD＝AE，连接BD，CE，试说明△ADB≌△AEC；
结论二：
（2）如图2，在（1）的条件下，若点E在BC边上，试说明DB⊥BC；
应用：
（3）如图3，在四边形ABCD中，∠ABC＝∠ADC＝90°，AB＝CB，∠BAD+∠BCD＝180°，连接BD，BD＝7cm，求四边形ABCD的面积．
查看答案和解析>>
科目： 来源： 题型：

【题目】以下说法合理的是（）
A. 小明在10次抛图钉的试验中发现3次钉尖朝上，由此他说钉尖朝上的概率是30%
B. 抛掷一枚普通的正六面体骰子，出现6的概率是的意思是每6次就有1次掷得6
C. 某彩票的中奖机会是2%，那么如果买100张彩票一定会有2张中奖。
D. 在一次课堂进行的试验中，甲、乙两组同学估计硬币落地后，正面朝上的概率分别为0．48和0．51。
查看答案和解析>>