【题目】如图,在![]() 中,
中, ![]() ,
, ![]() 的垂直平分线分别与
的垂直平分线分别与![]() ,
, ![]() 及
及![]() 的延长线相交于点
的延长线相交于点![]() ,
, ![]() ,
, ![]() ,且
,且![]() . ⊙O是
. ⊙O是![]() 的外接圆,
的外接圆, ![]() 的平分线交
的平分线交![]() 于点
于点![]() ,交⊙O于点
,交⊙O于点![]() ,连接
,连接![]() ,
, ![]() .
.
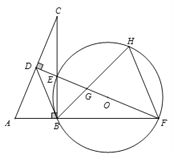
(1)求证: ![]() ;
;
(2)试判断![]() 与⊙O的位置关系,并说明理由;
与⊙O的位置关系,并说明理由;
(3)若![]() , 求
, 求![]() 的值.
的值.
参考答案:
【答案】(1)证明见解析;(2)![]() 与
与![]() 相切. 理由见解析;(3)
相切. 理由见解析;(3)![]() .
.
【解析】试题分析:
(1)两个三角形都是直角三角形,有一条直角边相等,只需要得到另一组对应角相等即可;
(2)连接OB,设法结合(1)的结论得到∠DBC=∠OBC,证明∠DBO=90°;
(3)由△HFB与△HBF是一对相似三角形,得到![]() ,而△HEF是一个等腰直角三角形,则需要求EF的长,在直角△BEF中BE=AB=1,故要求BF的长,又BF=BC,BC=BE+CE,CE=AE,在直角△ABE中求得AE的长.
,而△HEF是一个等腰直角三角形,则需要求EF的长,在直角△BEF中BE=AB=1,故要求BF的长,又BF=BC,BC=BE+CE,CE=AE,在直角△ABE中求得AE的长.
试题解析:
(1)∵DF⊥AC,△ABC为Rt△,
∴∠CED=∠FEB, ![]() .
.
∠ABC=∠EBF=Rt∠,
又![]() ,∴
,∴![]() (
(![]() ).
).
(2)![]() 与
与![]() 相切. 理由如下:
相切. 理由如下:
连接![]() , ∵DF是AB的中垂线,∠ABC=90°,∴DB=DC=DA,
, ∵DF是AB的中垂线,∠ABC=90°,∴DB=DC=DA,
∴∠DBC=∠C.
由(1)∠DCB=∠EFB,而∠EFB=∠OBF,∴∠DBC=∠OBF.
∴![]() ,
,
∴![]() .∴BD与⊙O相切.
.∴BD与⊙O相切.
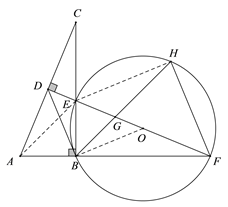
(3)连接![]() ,AE.
,AE.
∵BH是∠EBF的平分线,∴∠EBH=∠HBF=45°. ∠HFE=∠HBE=45°.
又∠GHF=∠FHB,∴△GHF∽△FHB,
∴![]() =
=![]() ,∴HG·HB=HF2.
,∴HG·HB=HF2.
∵⊙O是Rt△BEF的外接圆,∴EF为⊙O的直径,∴∠EHF=90°,
又∠HFE=45°,∴EH=HF. ∴EF2=EH2
∵DF是线段AC的垂直平分线,∴AE=CE,
又∵![]() ,∴AB=BE=1,∴AE=CE=
,∴AB=BE=1,∴AE=CE=![]() ,所以BF=BC=
,所以BF=BC=![]() ,
,
由勾股定理得, ![]() ,
,
∴![]() ,∴
,∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若m是方程2x2﹣3x﹣1=0的一个根,则6m2﹣9m+2017的值为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】保护环境,让我们从垃圾分类做起.某区环保部门为了提高宣传实效,抽样调查了部分居民小区一段时间内生活垃圾的分类情况(如图1),进行整理后,绘制了如下两幅尚不完整的统计图:
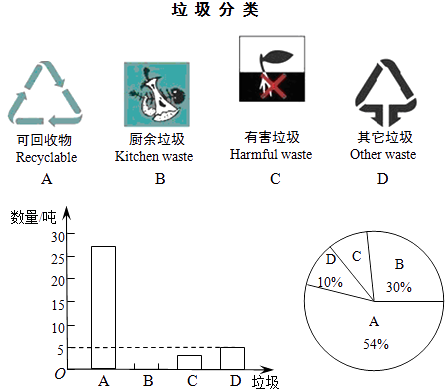
根据图表解答下列问题:
(1)请将图2﹣条形统计图补充完整;
(2)在图3﹣扇形统计图中,求出“D”部分所对应的圆心角等于度;
(3)在抽样数据中,产生的有害垃圾共有吨;
(4)调查发现,在可回收物中废纸垃圾约占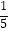 ,若每回收1吨废纸可再造好纸0.85吨.假设该城市每月产生的生活垃圾为10000吨,且全部分类处理,那么每月回收的废纸可再造好纸多少吨?
,若每回收1吨废纸可再造好纸0.85吨.假设该城市每月产生的生活垃圾为10000吨,且全部分类处理,那么每月回收的废纸可再造好纸多少吨? -
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题错误的个数有( )
①经过三个点一定可以作一个圆; ②三角形的外心到三角形各顶点的距离相等;
③同圆或等圆中,相等的圆心角所对的弧相等;④平分弦的直径垂直于弦.
A.1个B.2个C.3个D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在□
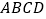 中,过点
中,过点 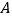 作
作  ⊥
⊥ 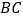 于点
于点 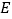 ,
, 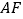 ⊥
⊥ 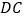 于点
于点  ,
, 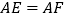 .
.
求证:四边形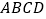 是菱形.
是菱形.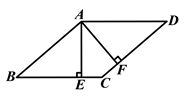
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一艘核潜艇在海面下500米的A点处测得俯角为
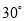 正前方的海底有黑匣子信号发出,继续在同一深度直线航行3000米后再次在B点处测得俯角为
正前方的海底有黑匣子信号发出,继续在同一深度直线航行3000米后再次在B点处测得俯角为 正前方的海底有黑匣子信号发出,求海底黑匣子C点处距离海面的深度.(保留根号)
正前方的海底有黑匣子信号发出,求海底黑匣子C点处距离海面的深度.(保留根号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:﹣(﹣1)=( )
A.1
B.﹣1
C.﹣2
D.±1
相关试题

