【题目】如图,已知AB为⊙O的直径,CD是弦,且AB![]() CD于点E。连接AC、OC、BC。
CD于点E。连接AC、OC、BC。
(1)求证: ![]() ACO=
ACO=![]() BCD。
BCD。
(2)若EB=![]() ,CD=
,CD=![]() ,求⊙O的直径。
,求⊙O的直径。

参考答案:
【答案】(1)详见解析;(2)⊙O的直径为26cm.
【解析】试题分析:(1)根据垂径定理可得CE=ED, ![]() ,由等弧所对的圆周角相等可得∠BCD=∠BAC,又因为△AOC是等腰三角形,即可得
,由等弧所对的圆周角相等可得∠BCD=∠BAC,又因为△AOC是等腰三角形,即可得![]() OAC=
OAC=![]() OCA,结论得证;(2)根据垂径定理可得CE=ED
OCA,结论得证;(2)根据垂径定理可得CE=ED![]() ,设⊙O的半径为Rcm,则OE= R
,设⊙O的半径为Rcm,则OE= R![]() 8,在Rt
8,在Rt![]() CEO中,根据勾股定理列出以R为未知数的方程,解方程即可求得圆的半径长,从而求得圆的直径的长.
CEO中,根据勾股定理列出以R为未知数的方程,解方程即可求得圆的半径长,从而求得圆的直径的长.
试题解析:
证明:(1)∵AB为⊙O的直径,CD是弦,且AB![]() CD于E,
CD于E,
∴CE=ED, ![]() ,
,
∴![]() BCD=
BCD=![]() BAC,
BAC,
∵OA=OC .
∴![]() OAC=
OAC=![]() OCA .
OCA .
∴![]() ACO=
ACO=![]() BCD .
BCD .
(2)设⊙O的半径为Rcm,则OE=OB![]() EB=R
EB=R![]() 8,
8,
CE=![]() CD=
CD=![]()
![]() 24=12,
24=12,
在Rt![]() CEO中,由勾股定理可得,
CEO中,由勾股定理可得,
OC![]() =OE
=OE![]() +CE
+CE![]() ,
,
即R![]() = (R
= (R![]() 8)
8) ![]() +12
+12![]() ,
,
解得 R=13.
∴2R=2![]() 13=26 .
13=26 .
答:⊙O的直径为26cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD,BE.
(1)求证:CE=AD;
(2)当D为AB中点时,四边形BECD是什么特殊四边形?说明你的理由;
(3)若D为AB中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?请说明你的理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线的对称轴是y轴,且点(2,2),(1,
 )在抛物线上,点P是抛物线上不与顶点N重合的一动点,过P作PA⊥x轴于A,PC⊥y轴于C,延长PC交抛物线于E,设M是O关于抛物线顶点N的对称点,D是C点关于N的对称点.
)在抛物线上,点P是抛物线上不与顶点N重合的一动点,过P作PA⊥x轴于A,PC⊥y轴于C,延长PC交抛物线于E,设M是O关于抛物线顶点N的对称点,D是C点关于N的对称点.(1)求抛物线的解析式及顶点N的坐标;
(2)求证:四边形PMDA是平行四边形;
(3)求证:△DPE∽△PAM,并求出当它们的相似比为
 时的点P的坐标.
时的点P的坐标.
-
科目: 来源: 题型:
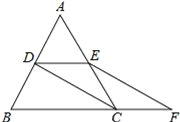
查看答案和解析>>【题目】如图,等边△ABC的边长是2,D、E分别为AB、AC的中点,过E点作EF∥DC交BC的延长线于点F,连接CD.
(1)求证:四边形CDEF是平行四边形;
(2)求EF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)﹣0.125×18
 ×8
×8(2)﹣24×(
 ﹣
﹣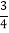 +
+ )
)(3)91
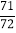 ×(﹣36)
×(﹣36)(4)﹣4×(﹣8
 )+(﹣8)×(﹣8
)+(﹣8)×(﹣8 )+12×(﹣8
)+12×(﹣8 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】观察下面一列数,探求其规律:

(1)请问第7个,第8个,第9个数分别是什么?
(2)第2007个数是什么?用n的代数式表示这一规律;
(3)如果这列数无限排列下去,越来越接近哪一个数?
-
科目: 来源: 题型:
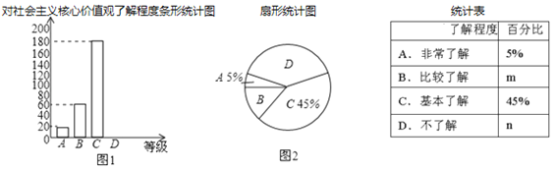
查看答案和解析>>【题目】为了调查学生对社会主义核心价值观的了解程度,我校在学生中做了一次抽样调查,调查结果共分为四个等级:A:非常了解;B:比较了解;C:基本了解;D:不了解.根据调查统计结果,绘制了下面的三种统计图表.
请结合统计图表,回答下列问题.
(1)本次参与调查的学生共有 人,m= ,n= ;
(2)图2所示的扇形统计图中D部分扇形所对应的圆心角是 度;
(3)请补全图1所示的条形统计图;
相关试题

