【题目】如图（1），在Rt△ABC中，∠A=90°，AC=AB=4，D，E分别是AB，AC的中点．若等腰Rt△ADE绕点A逆时针旋转，得到等腰Rt△AD1E1，如图（2），设旋转角为α（0＜α≤180°），记直线BD1与CE1的交点为P．

（1）求证：BD1=CE1；（2）当∠CPD1=2∠CAD1时，求CE1的长；

（3）连接PA，△PAB面积的最大值为　　．（直接填写结果）

参考答案：

【答案】（1）证明见解析（2） （3）2+2

【解析】试题分析：（1）先求证AC＝AB，再由中点可得出结果；
（2）由（1）的结论，在利用勾股定理计算即可；
（3）作出辅助线，利用勾股定理建立方程求出即可．

试题解析：

(1)∵∠A=90°，∠B=45°,

∴∠C=45°,

∴∠C=∠B ,

∴AC=AB,

∵D，E分别是AB，AC的中点 ,

∴CE= AC, BD=AB

∴BD= CE

(2)由(1)知△ABD1≌△ACE1，可证∠CPD1=90°,

∴∠CAD1=45°，∠BAD1=135°

在△ABD1中，可以求得BD12=20+8

∴CE12=20+8

(3) 作PG⊥AB，交AB所在直线于点G，如图

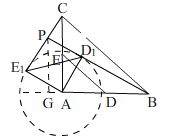
∵D1，E1在以A为圆心，AD为半径的圆上，
当BD1所在直线与⊙A相切时，直线BD1与CE1的交点P到直线AB的距离最大，
此时四边形AD1PE1是正方形，PD1=2，
则BD1=

∴∠ABP=30°，
∴PB=2+

∴点P到AB所在直线的距离的最大值为：PG=1+，

∴△PAB的面积最大值为AB×PG=2+.

故答案是：2+.

关闭