【题目】某学校为了解学生对新闻、体育、动画、娱乐、戏曲五类电视节目最喜爱的情况,随机调查了若干名学生,根据调查数据进行整理,绘制了如下的不完整统计图:

请你根据以上的信息,回答下列问题:
(1) 本次共调查了_____名学生,其中最喜爱戏曲的有_____人;在扇形统计图中,最喜爱体育的对应扇形的圆心角大小是______;
(2) 根据以上统计分析,估计该校2000名学生中最喜爱新闻的人数.
参考答案:
【答案】(1)50,3,72°;(2)160人.
【解析】
试题分析:(1)用喜爱新闻的人数除以喜爱新闻的人数所占的百分比即可得这次调查的学生人数;用这次调查的学生人数乘以喜爱戏曲人数所占的百分比即可得喜爱戏曲的学生人数;先求得喜爱娱乐活动所占的百分比,再求得喜爱体育学生所占的的百分比,用360°乘以喜爱体育学生所占的的百分比即可得喜爱体育的对应扇形的圆心角的度数.(2)用2000乘以喜爱新闻的人数所占的百分比即可得该校喜爱新闻的学生人数.
试题解析:(1)本次共调查学生:4÷8%=50(人),最喜爱戏曲的人数为:50×6%=3(人),∵“娱乐”类人数占被调查人数的百分比为:![]() ,
,
∴“体育”类人数占被调查人数的百分比为:1-8%-30%-36%-6%=20%,
在扇形统计图中,最喜爱体育的对应扇形圆心角大小事360°×20%=72°;
(2)2000×8%=160(人).
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题12分)若点A、B在数轴上分别表示实数a、b,则我们可以定义|a-b|为A、B两点之间的距离,表示为|AB|=|a-b|.根据这个定义回答下列问题:
(1)数轴上表示2和5的两点之间的距离是______ ,表示-2和-5的两点之间的距离是______ ;表示1和-3的两点之间的距离是______ ;表示x和-1的两点A和B之间的距离是_____ ;
(2)如果|x+3|=2,求
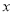 的值;
的值;(3)代数式|x+3|+|x-2|最小值是______ ;方程|x+3|+|x-2|=7的解为 。
-
科目: 来源: 题型:
查看答案和解析>>【题目】若有理数x、y满足|x|=5,|y|=2,且|x+y|=x+y,求x﹣y的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若∠α=38o42',则∠α的补角等于_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将一个正方体的表面沿某些棱剪开,展成一个平面图形,至少要剪开( )条棱.
A.3
B.5
C.7
D.9 -
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分11分)已知∠ABC=90°,D是直线AB上的点,AD=BC.
(1)如图1,过点A作AF⊥AB,并截取AF=BD,连接DC、DF、CF,判断△CDF的形状并证明;
(2)如图2,E是直线BC上一点,且CE=BD,直线AE、CD相交于点P,∠APD的度数是一个固定的值吗?若是,请求出它的度数;若不是,请说明理由.
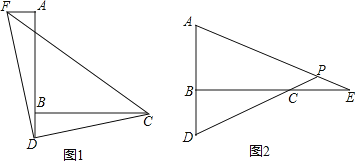
-
科目: 来源: 题型:
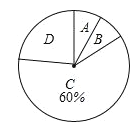
查看答案和解析>>【题目】(2016山东潍坊第20题)今年5月,某大型商业集团随机抽取所属的m家商业连锁店进行评估,将各连锁店按照评估成绩分成了A、B、C、D四个等级,绘制了如图尚不完整的统计图表.
评估成绩n(分)
评定等级
频数
90≤n≤100
A
2
80≤n<90
B
70≤n<80
C
15
n<70
D
6
根据以上信息解答下列问题:
(1)求m的值;
(2)在扇形统计图中,求B等级所在扇形的圆心角的大小;(结果用度、分、秒表示)
(3)从评估成绩不少于80分的连锁店中任选2家介绍营销经验,求其中至少有一家是A等级的概率.
相关试题

