【题目】(本小题满分11分)已知∠ABC=90°,D是直线AB上的点,AD=BC.
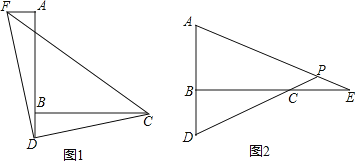
(1)如图1,过点A作AF⊥AB,并截取AF=BD,连接DC、DF、CF,判断△CDF的形状并证明;
(2)如图2,E是直线BC上一点,且CE=BD,直线AE、CD相交于点P,∠APD的度数是一个固定的值吗?若是,请求出它的度数;若不是,请说明理由.
参考答案:
【答案】见解析
【解析】(1)△CDF是等腰直角三角形,(1分)
理由如下:
∵AF⊥AD,∠ABC=90°,∴∠FAD=∠DBC,(2分)
在△FAD与△DBC中,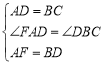 ,∴△FAD≌△DBC(SAS),(3分)
,∴△FAD≌△DBC(SAS),(3分)
∴FD=DC,∴△CDF是等腰三角形,(4分)
∵△FAD≌△DBC,∴∠FDA=∠DCB,
∵∠BDC+∠DCB=90°,∴∠BDC+∠FDA=90°,∴△CDF是等腰直角三角形.(5分)
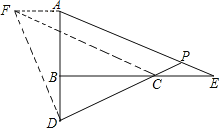
(2)作AF⊥AB于A,使AF=BD,连接DF,CF,如图,
∵AF⊥AD,∠ABC=90°,∴∠FAD=∠DBC,
在△FAD与△DBC中,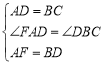 ,
,
∴△FAD≌△DBC(SAS),∴FD=DC,∴△CDF是等腰三角形,(6分)
∵△FAD≌△DBC,∴∠FDA=∠DCB,
∵∠BDC+∠DCB=90°,∴∠BDC+∠FDA=90°,
∴△CDF是等腰直角三角形,(7分)
∴∠FCD=45°,(8分)
∵AF∥CE,且AF=CE,∴四边形AFCE是平行四边形,(10分)
∴AE∥CF,∴∠APD=∠FCD=45°.(11分)
-
科目: 来源: 题型:
查看答案和解析>>【题目】若∠α=38o42',则∠α的补角等于_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校为了解学生对新闻、体育、动画、娱乐、戏曲五类电视节目最喜爱的情况,随机调查了若干名学生,根据调查数据进行整理,绘制了如下的不完整统计图:

请你根据以上的信息,回答下列问题:
(1) 本次共调查了_____名学生,其中最喜爱戏曲的有_____人;在扇形统计图中,最喜爱体育的对应扇形的圆心角大小是______;
(2) 根据以上统计分析,估计该校2000名学生中最喜爱新闻的人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将一个正方体的表面沿某些棱剪开,展成一个平面图形,至少要剪开( )条棱.
A.3
B.5
C.7
D.9 -
科目: 来源: 题型:
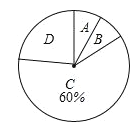
查看答案和解析>>【题目】(2016山东潍坊第20题)今年5月,某大型商业集团随机抽取所属的m家商业连锁店进行评估,将各连锁店按照评估成绩分成了A、B、C、D四个等级,绘制了如图尚不完整的统计图表.
评估成绩n(分)
评定等级
频数
90≤n≤100
A
2
80≤n<90
B
70≤n<80
C
15
n<70
D
6
根据以上信息解答下列问题:
(1)求m的值;
(2)在扇形统计图中,求B等级所在扇形的圆心角的大小;(结果用度、分、秒表示)
(3)从评估成绩不少于80分的连锁店中任选2家介绍营销经验,求其中至少有一家是A等级的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将二次函数y=x2﹣4x+5化成y=(x﹣h)2+k的形式,则y= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了传承优秀传统文化,某校开展“经典诵读”比赛活动,诵读材料有《论语》,《三字经》,《弟子规》(分别用字母A,B,C依次表示这三个诵读材料),将A,B,C这三个字母分别写在3张完全相同的不透明卡片的正面上,把这3张卡片背面朝上洗匀后放在桌面上.小明和小亮参加诵读比赛,比赛时小明先从中随机抽取一张卡片,记录下卡片上的内容,放回后洗匀,再由小亮从中随机抽取一张卡片,选手按各自抽取的卡片上的内容进行诵读比赛.
(1)小明诵读《论语》的概率是 ;
(2)请用列表法或画树状图(树形图)法求小明和小亮诵读两个不同材料的概率.
相关试题

