【题目】如图,已知AB∥CD,请分别判断下面四个图形中∠APC、∠PAB、∠PCD之间的关系.
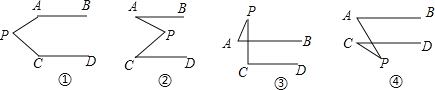
(1)写出相应的四个结论;
(2)请证明你所得的第③个图形的结论.
参考答案:
【答案】(1)①∠APC+∠PAB+∠PCD=360°,
②∠APC=∠PAB+∠PCD,
③∠APC=∠PCD﹣∠PAB,
④∠APC=∠PAB﹣∠PCD;
(2)见解析
【解析】
试题分析:分别过点P作PE∥AB,然后根据平行线的性质解答即可.
(1)解:①∠APC+∠PAB+∠PCD=360°,
②∠APC=∠PAB+∠PCD,
③∠APC=∠PCD﹣∠PAB,
④∠APC=∠PAB﹣∠PCD;
(2)证明:如图,过点P作PE∥AB,
∴∠APE=180°﹣∠PAB,
∵AB∥CD,
∴PE∥CD,
∴∠CPE=180°﹣∠PCD,
∴∠APC=∠APE﹣∠CPE=(180°﹣∠PAB)﹣(180°﹣∠PCD)=∠PCD﹣∠PAB.

-
科目: 来源: 题型:
查看答案和解析>>【题目】若2a-b=5,a-2b=4,则a-b的值为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算(﹣a3b) 2的结果是( )
A. a5b2 B. ﹣a3b2 C. 2a6b2 D. a6b2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等边△ABC内有一点D,AD=5,BD=6,CD=4,将△ABD绕A点逆时针旋转,使AB与AC重合,点D旋转至点E,求∠CDE的余弦值.

-
科目: 来源: 题型:
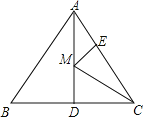
查看答案和解析>>【题目】如图,等边△ABC的边长为6,AD是BC边上的中线,M是AD上的动点,E是AC边上一点,若AE=2,EM+CM的最小值为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,△ABC中,AC=BC,∠ACB=90°,D为AB的中点,若E在直线AC上任意一点,DF⊥DE,交直线BC于F点.G为EF的中点,延长CG交AB于点H.

(1)若E在边AC上.
①试说明DE=DF;
②试说明CG=GH;
(2)若AE=3,CH=5.求边AC的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一件服装的标价为300元,打八折销售后可获利60元,则该件服装的成本价是_________元.
相关试题

