【题目】已知,△ABC中,AC=BC,∠ACB=90°,D为AB的中点,若E在直线AC上任意一点,DF⊥DE,交直线BC于F点.G为EF的中点,延长CG交AB于点H.

(1)若E在边AC上.
①试说明DE=DF;
②试说明CG=GH;
(2)若AE=3,CH=5.求边AC的长.
参考答案:
【答案】(1)①证明见解析;②证明见解析;(2)AC=7或1.
【解析】
试题分析:(1)①连接CD,推出CD=AD,∠CDF=∠ADE,∠A=∠DCB,证△ADE≌△CDF即可;②连接DG,根据直角三角形斜边上中线求出CG=EG=GF=DG,推出∠GCD=∠GDC,推出∠GDH=∠GHD,推出DG=GH即可;
(2)求出EF=5,根据勾股定理求出EC,即可得出答案.
试题解析:(1)①连接CD,∵∠ACB=90°,D为AB的中点,AC=BC,∴CD=AD=BD,又∵AC=BC,∴CD⊥AB,∴∠EDA+∠EDC=90°,∠DCF=∠DAE=45°,∵DF⊥DE,∴∠EDF=∠EDC+∠CDF=90°,∴∠ADE=∠CDF,在△ADE和△CDF中,∵∠A=∠DCF,AD=CD,∠ADE=∠CDF,∴△ADE≌△CDF,∴DE=DF;
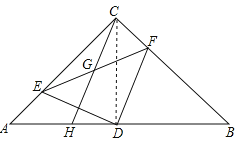
②连接DG,∵∠ACB=90°,G为EF的中点,∴CG=EG=FG,∵∠EDF=90°,G为EF的中点,∴DG=EG=FG,∴CG=DG,∴∠GCD=∠CDG.又∵CD⊥AB,∴∠CDH=90°,∴∠GHD+∠GCD=90°,∠HDG+∠GDC=90°,∴∠GHD=∠HDG,∴GH=GD,∴CG=GH;
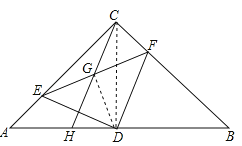
(2)如图,当E在线段AC上时,∵CG=GH=EG=GF,∴CH=EF=5,∵△ADE≌△CDF,∴AE=CF=3,∴在Rt△ECF中,由勾股定理得:CE=![]() =4,∴AC=AE+EC=3+4=7;
=4,∴AC=AE+EC=3+4=7;
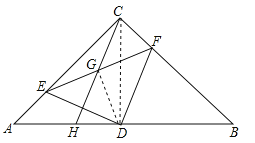
如图,当E在线段CA延长线时,AC=EC﹣AE=4﹣3=1,综合上述:AC=7或1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等边△ABC内有一点D,AD=5,BD=6,CD=4,将△ABD绕A点逆时针旋转,使AB与AC重合,点D旋转至点E,求∠CDE的余弦值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB∥CD,请分别判断下面四个图形中∠APC、∠PAB、∠PCD之间的关系.
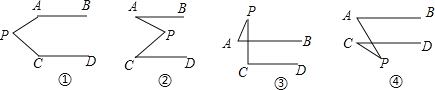
(1)写出相应的四个结论;
(2)请证明你所得的第③个图形的结论.
-
科目: 来源: 题型:
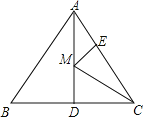
查看答案和解析>>【题目】如图,等边△ABC的边长为6,AD是BC边上的中线,M是AD上的动点,E是AC边上一点,若AE=2,EM+CM的最小值为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一件服装的标价为300元,打八折销售后可获利60元,则该件服装的成本价是_________元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:3a3﹣12a2b+12ab2= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】若-2amb4与3a2bn+2是同类项,则m+n=__________.
相关试题

