【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() (
(![]() 为常数,且
为常数,且![]() )的图象交于A(1,a)、B两点.
)的图象交于A(1,a)、B两点.
(1)求反比例函数的表达式及点B的坐标;
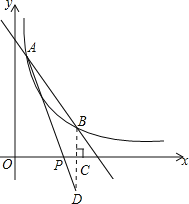
(2)在x轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标及△PAB的面积.

参考答案:
【答案】(1)![]() ,B(3,1);(2)P(
,B(3,1);(2)P(![]() ,0),
,0),![]() .
.
【解析】
试题分析:(1)把点A(1,a)代入一次函数y=﹣x+4,即可得出a,再把点A坐标代入反比例函数![]() ,即可得出k,两个函数解析式联立求得点B坐标;
,即可得出k,两个函数解析式联立求得点B坐标;
(2)作点B作关于x轴的对称点D,交x轴于点C,连接AD,交x轴于点P,此时PA+PB的值最小,求出直线AD的解析式,令y=0,即可得出点P坐标.
试题解析:(1)把点A(1,a)代入一次函数y=﹣x+4,得a=﹣1+4,解得a=3,∴A(1,3),点A(1,3)代入反比例函数![]() ,得k=3,∴反比例函数的表达式
,得k=3,∴反比例函数的表达式![]() ,两个函数解析式联立列方程组得
,两个函数解析式联立列方程组得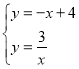 ,解得
,解得![]() 或
或![]() ,∴点B坐标(3,1);
,∴点B坐标(3,1);
(2)作点B作关于x轴的对称点D,交x轴于点C,连接AD,交x轴于点P,此时PA+PB的值最小,∴D(3,﹣1),设直线AD的解析式为y=mx+n,把A,D两点代入得,![]() ,解得m=﹣2,n=5,∴直线AD的解析式为y=﹣2x+5,令y=0,得x=
,解得m=﹣2,n=5,∴直线AD的解析式为y=﹣2x+5,令y=0,得x=![]() ,∴点P坐标(
,∴点P坐标(![]() ,0),S△PAB=S△ABD﹣S△PBD=
,0),S△PAB=S△ABD﹣S△PBD=![]() ×2×2﹣
×2×2﹣![]() ×2×
×2×![]() =2﹣
=2﹣![]() =1.5.
=1.5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以△ABC的BC边上一点O为圆心,经过A,C两点且与BC边交于点E,点D为CE的下半圆弧的中点,连接AD交线段EO于点F,若AB=BF.
(1)求证:AB是⊙O的切线;
(2)若CF=4,DF=
 ,求⊙O的半径r及sinB.
,求⊙O的半径r及sinB.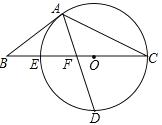
-
科目: 来源: 题型:
查看答案和解析>>【题目】线段CD是由线段AB平移得到的.点A(﹣2,5)的对应点为C(3,7),则点B(﹣3,0)的对应点D的坐标为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,将函数y=2x2的图象先向右平移1个单位,再向上平移5个单位得到图象的函数关系式是( )
A.y=2(x﹣1)2﹣5
B.y=2(x﹣1)2+5
C.y=2(x+1)2﹣5
D.y=2(x+1)2+5 -
科目: 来源: 题型:
查看答案和解析>>【题目】(_________)2=m4b6;______ ×3n-1=32n+3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于反比例函数y=﹣
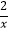 ,下列说法正确的是( )
,下列说法正确的是( )
A.图像在第一、三象限
B.图像经过(2,1)
C.在每个象限中,y随x的增大而减小
D.当x>1时,﹣2<y<0 -
科目: 来源: 题型:
查看答案和解析>>【题目】草莓是云南多地盛产的一种水果,今年某水果销售店在草莓销售旺季,试销售成本为每千克20元的草莓,规定试销期间销售单价不低于成本单价,也不高于每千克40元,经试销发现,销售量y(千克)与销售单价x(元)符合一次函数关系,如图是y与x的函数关系图象.
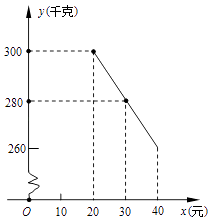
(1)求y与x的函数关系式;
(2)求出自变量x的取值范围.
相关试题

