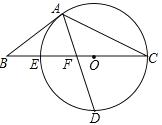
【题目】如图,以△ABC的BC边上一点O为圆心,经过A,C两点且与BC边交于点E,点D为CE的下半圆弧的中点,连接AD交线段EO于点F,若AB=BF.
(1)求证:AB是⊙O的切线;
(2)若CF=4,DF=![]() ,求⊙O的半径r及sinB.
,求⊙O的半径r及sinB.
参考答案:
【答案】(1)证明见解析;(2)r=3,sinB=![]() .
.
【解析】
试题分析:(1)连接OA、OD,如图,根据垂径定理得OD⊥BC,则∠D+∠OFD=90°,再由AB=BF,OA=OD得到∠BAF=∠BFA,∠OAD=∠D,加上∠BFA=∠OFD,所以∠OAD+∠BAF=90°,则OA⊥AB,然后根据切线的判定定理即可得到AB是⊙O切线;
(2)先表示出OF=4﹣r,OD=r,在Rt△DOF中利用勾股定理建立方程,解方程得到r的值,那么OA=3,OF=CF﹣OC=4﹣3=1,BO=BF+FO=AB+1.
然后在Rt△AOB中利用勾股定理,得到AB的值,再根据三角函数定义求出sinB.
试题解析:(1)证明:连接OA、OD,如图,∵点D为CE的下半圆弧的中点,∴OD⊥BC,∴∠EOD=90°,∵AB=BF,OA=OD,∴∠BAF=∠BFA,∠OAD=∠D,而∠BFA=∠OFD,∴∠OAD+∠BAF=∠D+∠BFA=90°,即∠OAB=90°,∴OA⊥AB,∴AB是⊙O切线;
(2)解:OF=CF﹣OC=4﹣r,OD=r,DF=![]() ,在Rt△DOF中,
,在Rt△DOF中,![]() ,即
,即![]() ,解得:r=3或r=1(舍去);∴半径r=3,∴OA=3,OF=CF﹣OC=4﹣3=1,BO=BF+FO=AB+1.在Rt△AOB中,
,解得:r=3或r=1(舍去);∴半径r=3,∴OA=3,OF=CF﹣OC=4﹣3=1,BO=BF+FO=AB+1.在Rt△AOB中,![]() ,∴
,∴![]() ,∴AB=4,OB=5,∴sinB=
,∴AB=4,OB=5,∴sinB=![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a2=25,|b|=3,则a+b的值是( )
A.﹣8
B.±8
C.±2
D.±8或±2 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程(a﹣1)x2﹣2x+1=0有两个不相等的实数根,则a的取值范围是( )
A.a<2
B.a>2
C.a<﹣2
D.a<2且a≠1 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一条直线分别与直线BE、直线CE、直线BF、直线CF相交于点A,G,H,D且∠1=∠2,∠B=∠C
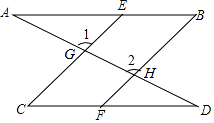
(1)找出图中相互平行的线,说说它们之间为什么是平行的;
(2)证明:∠A=∠D. -
科目: 来源: 题型:
查看答案和解析>>【题目】线段CD是由线段AB平移得到的.点A(﹣2,5)的对应点为C(3,7),则点B(﹣3,0)的对应点D的坐标为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,将函数y=2x2的图象先向右平移1个单位,再向上平移5个单位得到图象的函数关系式是( )
A.y=2(x﹣1)2﹣5
B.y=2(x﹣1)2+5
C.y=2(x+1)2﹣5
D.y=2(x+1)2+5 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数
 的图象与反比例函数
的图象与反比例函数 (
( 为常数,且
为常数,且 )的图象交于A(1,a)、B两点.
)的图象交于A(1,a)、B两点.(1)求反比例函数的表达式及点B的坐标;
(2)在x轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标及△PAB的面积.

相关试题

