【题目】已知,如图,二次函数y=ax2+2ax﹣3a(a≠0)图象的顶点为H,与x轴交于A、B两点(B在A点右侧),点H、B关于直线l: ![]() 对称.
对称. 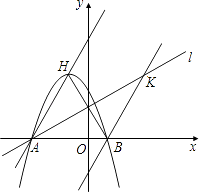
(1)求A、B两点坐标,并证明点A在直线l上;
(2)求二次函数解析式; 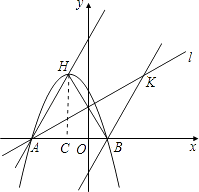
(3)过点B作直线BK∥AH交直线l于K点,M、N分别为直线AH和直线l上的两个动点,连接HN、NM、MK,求HN+NM+MK和的最小值. 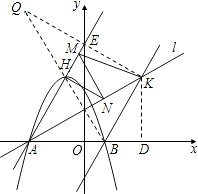
参考答案:
【答案】
(1)解:依题意,得ax2+2ax﹣3a=0(a≠0),
两边都除以a得:
即x2+2x﹣3=0,
解得x1=﹣3,x2=1,
∵B点在A点右侧,
∴A点坐标为(﹣3,0),B点坐标为(1,0),
答:A、B两点坐标分别是(﹣3,0),(1,0)
证明:∵直线l: ![]() ,
,
当x=﹣3时, ![]() ,
,
∴点A在直线l上
(2)解:∵点H、B关于过A点的直线l: ![]() 对称,
对称,
∴AH=AB=4,
过顶点H作HC⊥AB交AB于C点,
则 ![]() ,
, ![]() ,
,
∴顶点 ![]() ,
,
代入二次函数解析式,解得 ![]() ,
,
∴二次函数解析式为 ![]() ,
,
答:二次函数解析式为 ![]()
(3)解:直线AH的解析式为 ![]() ,
,
直线BK的解析式为 ![]() ,
,
由 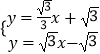 ,
,
解得 ![]() ,
,
即 ![]() ,
,
则BK=4,
∵点H、B关于直线AK对称,K(3,2 ![]() ),
),
∴HN+MN的最小值是MB,
过K作KD⊥x轴于D,作点K关于直线AH的对称点Q,连接QK,交直线AH于E,
则QM=MK, ![]() ,AE⊥QK,
,AE⊥QK,
∴根据两点之间线段最短得出BM+MK的最小值是BQ,即BQ的长是HN+NM+MK的最小值,
∵BK∥AH,
∴∠BKQ=∠HEQ=90°,
由勾股定理得QB= ![]() =
= ![]() =8,
=8,
∴HN+NM+MK的最小值为8,
答:HN+NM+MK和的最小值是8.
【解析】(1)求出方程ax2+2ax﹣3a=0(a≠0),即可得到A点坐标和B点坐标;把A的坐标代入直线l即可判断A是否在直线上;(2)根据点H、B关于过A点的直线l: ![]() 对称,得出AH=AB=4,过顶点H作HC⊥AB交AB于C点,求出AC和HC的长,得出顶点H的坐标,代入二次函数解析式,求出a,即可得到二次函数解析式;(3)解方程组
对称,得出AH=AB=4,过顶点H作HC⊥AB交AB于C点,求出AC和HC的长,得出顶点H的坐标,代入二次函数解析式,求出a,即可得到二次函数解析式;(3)解方程组 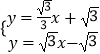 ,即可求出K的坐标,根据点H、B关于直线AK对称,得出HN+MN的最小值是MB,过点K作直线AH的对称点Q,连接QK,交直线AH于E,得到BM+MK的最小值是BQ,即BQ的长是HN+NM+MK的最小值,由勾股定理得QB=8,即可得出答案.
,即可求出K的坐标,根据点H、B关于直线AK对称,得出HN+MN的最小值是MB,过点K作直线AH的对称点Q,连接QK,交直线AH于E,得到BM+MK的最小值是BQ,即BQ的长是HN+NM+MK的最小值,由勾股定理得QB=8,即可得出答案.
【考点精析】解答此题的关键在于理解解二元一次方程组的相关知识,掌握二元一次方程组:①代入消元法;②加减消元法,以及对抛物线与坐标轴的交点的理解,了解一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠A=90°,O是BC边上一点,以O为圆心的半圆分别与AB、AC边相切于D、E两点,连接OD.已知BD=2,AD=3.

求:
(1)tanC;
(2)图中两部分阴影面积的和. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知,矩形ABCD中,AB=4cm,BC=8cm,AC的垂直平分线EF分别交AD、BC于点E、F,垂足为O.
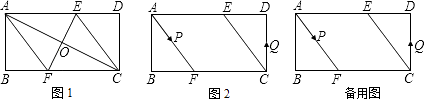
(1)如图1,连接AF、CE.求证四边形AFCE为菱形,并求AF的长;
(2)如图2,动点P、Q分别从A、C两点同时出发,沿△AFB和△CDE各边匀速运动一周.即点P自A→F→B→A停止,点Q自C→D→E→C停止.在运动过程中, ①已知点P的速度为每秒5cm,点Q的速度为每秒4cm,运动时间为t秒,当A、C、P、Q四点为顶点的四边形是平行四边形时,求t的值.
②若点P、Q的运动路程分别为a、b(单位:cm,ab≠0),已知A、C、P、Q四点为顶点的四边形是平行四边形,求a与b满足的数量关系式. -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面一段:
计算
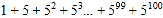
观察发现,上式从第二项起,每项都是它前面一项的
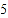 倍,如果将上式各项都乘以
倍,如果将上式各项都乘以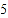 ,所得新算式中除个别项外,其余与原式中的项相同,于是两式相减将使差易于计算.
,所得新算式中除个别项外,其余与原式中的项相同,于是两式相减将使差易于计算.解:设
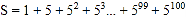 ,①
,①则
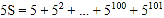 ,②
,②②-①得
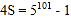 ,则
,则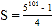 .
.上面计算用的方法称为“错位相减法”,如果一列数,从第二项起每一项与前一项之比都相等(本例中是都等于
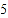 ),那么这列数的求和问题,均可用上述“错位相减”法来解决.
),那么这列数的求和问题,均可用上述“错位相减”法来解决.下面请你观察算式
 是否具备上述规律?若是,请你尝试用“错位相减”法计算上式的结果.
是否具备上述规律?若是,请你尝试用“错位相减”法计算上式的结果. -
科目: 来源: 题型:
查看答案和解析>>【题目】一组数据7,2,5,4,2的方差为a,若再增加一个数据4,这6个数据的方差为b,则a与b的大小关系是( )
A. a>b B. a=b C. a<b D. 以上都有可能
-
科目: 来源: 题型:
查看答案和解析>>【题目】
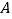 市、
市、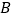 市和
市和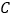 市分别有某种机器
市分别有某种机器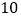 台、
台、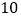 台、
台、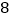 台,现在决定把这些机器支援给
台,现在决定把这些机器支援给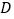 市
市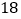 台,
台,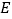 市
市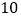 台.己知调运机器的费用如表所示.
台.己知调运机器的费用如表所示.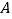 市
市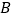 市
市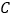 市
市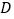 市
市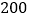 元/台
元/台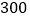 元/台
元/台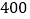 元/台
元/台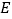 市
市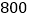 元/台
元/台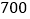 元/台
元/台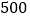 元/台
元/台设从
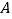 市、
市、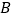 市各调
市各调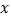 台到
台到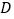 市.
市.(1)
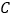 市调运到
市调运到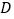 市的机器为________台 (用含
市的机器为________台 (用含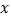 的式子表示);
的式子表示);(2)
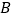 市调运到
市调运到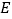 市的机器的费用为________元(用含
市的机器的费用为________元(用含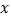 的式子表示,并化简);
的式子表示,并化简);(3)求调运完毕后的总运费(用
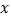 的式子表示,并化简);
的式子表示,并化简);(4)当
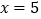 和
和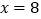 时,哪种调运方式总运费少?少多少?
时,哪种调运方式总运费少?少多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠B=∠C=36°,AB的垂直平分线交BC于点D,交AB于点H,AC的垂直平分线交BC于点E,交AC于点G,连接AD,AE,则下列结论错误的是( )
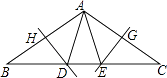
A.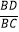 =
= 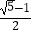
B.AD,AE将∠BAC三等分
C.△ABE≌△ACD
D.S△ADH=S△CEG
相关试题

