【题目】完成下面推理过程:
已知:如图,已知∠1 =∠2,∠B =∠C,
求证:AB∥CD.
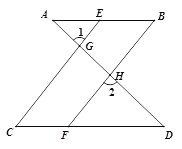
证明∵∠1 =∠2(已知),
且∠1 =∠CGD( ),
∴∠2 =∠CGD(等量代换).
∴CE∥BF( ).
∴∠ =∠C( ).
又∵∠B =∠C(已知),
∴∠ =∠B(等量代换).
∴AB∥CD( ).
参考答案:
【答案】对顶角相等. 同位角相等,两直线平行. ∠BFD, 两直线平行,同位角相等, ∠BFD, 内位角相等,两直线平行.
【解析】试题分析:根据对顶角相等,易得∠1=∠CGD,通过等量代换得到∠2=∠CGD,而其互为同位角,据此可得CE和BF的位置关系;再根据平行线的性质,结合∠BFD和∠C为同位角,∠B=∠C,可得∠B和∠BFD的关系,而∠B和∠BFD互为内错角,至此问题不难解决.
试题解析:∵∠1=∠2(已知),
且∠1=∠CGD(对顶角相等),
∴∠2=∠CGD(等量代换),
∴CE∥BF(同位角相等,两直线平行),
∴∠BFD=∠C(两直线平行,同位角相等),
又∵∠B=∠C(已知),
∴∠BFD=∠B(等量代换).
∴AB∥CD(内错角相等,两直线平行).
故答案为:对顶角相等. 同位角相等,两直线平行. ∠BFD, 两直线平行,同位角相等, ∠BFD, 内位角相等,两直线平行.
-
科目: 来源: 题型:
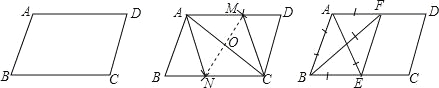
查看答案和解析>>【题目】如图,在给定的一张平行四边形纸片上作一个菱形.甲、乙两人的作法如下:
甲:连接AC,作AC的垂直平分线MN分别交AD,AC,BC于M,O,N,连接AN,CM,则四边形ANCM是菱形.
乙:分别作∠A,∠B的平分线AE,BF,分别交BC,AD于E,F,连接EF,则四边形ABEF是菱形.
根据两人的作法可判断( )
A.甲正确,乙错误 B.乙正确,甲错误
C.甲、乙均正确 D.甲、乙均错误
-
科目: 来源: 题型:
查看答案和解析>>【题目】尺规作图作一个角的角平分线的依据是( ).
A. SASB. ASAC. AASD. SSS
-
科目: 来源: 题型:
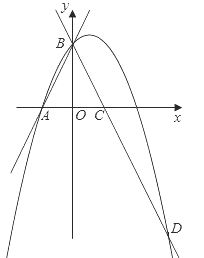
查看答案和解析>>【题目】如图,直线y=2x+2与x轴交于点A,与y轴交于点B,把△AOB沿y轴翻折,点A落到点C,过点B的抛物线y=-x2+bx+c与直线BC交于点D(3,-4).
(1)求直线BD和抛物线的解析式;
(2)在第一象限内的抛物线上,是否存在一点M,作MN垂直于x轴,垂足为点N,使得以M、O、N为顶点的三角形与△BOC相似?若存在,求出点M的坐标;若不存在,请说明理由;
(3)在直线BD上方的抛物线上有一动点P,过点P作PH垂直于x轴,交直线BD于点H,当四边形BOHP是平行四边形时,试求动点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x+y=6,xy=4,则x2y+xy2的值为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】多项式x2y(a-b)-xy(b-a)+y(a-b)提公因式后,另一个因式为_____________
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB、CD分别表示甲、乙两建筑物的高,从A点测得D点的仰角为30°,从B点测得D点的仰角为60°,已知两楼之间的距离为27米.求甲、乙两建筑物的高AB、CD.(结果精确到个位)(参考数据:
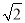 ≈1.4,
≈1.4, ≈1.7)
≈1.7)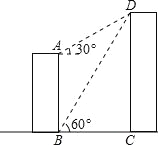
相关试题

