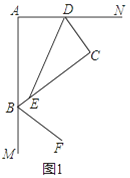
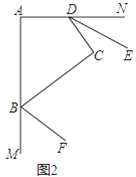
【题目】如图1,放置的一副三角尺,将含45°角的三角尺斜边中点O为旋转中心,逆时针旋转30°得到如图2,连接OB、OD、AD. 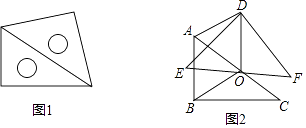
(1)求证:△AOB≌△AOD;
(2)试判定四边形ABOD是什么四边形,并说明理由.
参考答案:
【答案】
(1)证明:根据题意得:∠BAC=60°,∠ABC=∠EDF=90°,EF=AC,
∵O为AC的中点,
∴OB= ![]() AC=OA,OD=
AC=OA,OD= ![]() EF=
EF= ![]() AC=OB,OD⊥EF,
AC=OB,OD⊥EF,
∴△AOB是等边三角形,
∴∠AOB=60°,AB=OB=OA,
由旋转的性质得:∠AOE=30°,
∴∠AOD=90°﹣30°=60°,
在△AOB和△AOD中, 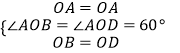 ,
,
∴△AOB≌△AOD(SAS)
(2)解:四边形ABOD是菱形;理由如下:
∵△AOB≌△AOD,
∴AB=AD,
∴AB=AD=OB=OD,
∴四边形ABOD是菱形
【解析】(1)根据题意得:∠BAC=60°,∠ABC=∠EDF=90°,EF=AC,由直角三角形斜边上的中线性质得出OB= ![]() AC=OA,OD=
AC=OA,OD= ![]() EF=
EF= ![]() AC=OB,由等腰三角形的性质得出OD⊥EF,证出△AOB是等边三角形,得出∠AOB=60°,由旋转的性质得:∠AOE=30°,证出∠AOD=60°,由SAS证明△AOB≌△AOD即可;(2)由全等三角形的性质得出AB=AD=OB=OD,即可得出四边形ABOD是菱形.
AC=OB,由等腰三角形的性质得出OD⊥EF,证出△AOB是等边三角形,得出∠AOB=60°,由旋转的性质得:∠AOE=30°,证出∠AOD=60°,由SAS证明△AOB≌△AOD即可;(2)由全等三角形的性质得出AB=AD=OB=OD,即可得出四边形ABOD是菱形.
【考点精析】解答此题的关键在于理解旋转的性质的相关知识,掌握①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了.
-
科目: 来源: 题型:
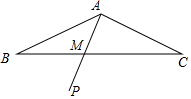
查看答案和解析>>【题目】在△ABC中,AB=AC,∠BAC=150°,点A到BC的距离为1,与AB重合的一条射线AP,从AB开始,以每秒15°的速度绕点A逆时针匀速旋转,到达AC后立即以相同的速度返回AB,到达后立即重复上述旋转过程,设AP与BC边的交点为M,旋转2019秒时,BM= , CM= .
-
科目: 来源: 题型:
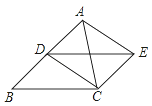
查看答案和解析>>【题目】已知,如图,点D是△ABC的边AB的中点,四边形BCED是平行四边形,
(1)求证:四边形ADCE是平行四边形;
(2)当△ABC满足什么条件时,平行四边形ADCE是矩形?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知凸四边形ABCD中,∠A=∠C=90°.
(1)如图1,若DE平分∠ADC,BF平分∠ABC的邻补角,判断DE与BF位置关系并证明.
(2)如图2,若BF、DE分别平分∠ABC、∠ADC的邻补角,判断DE与BF位置关系并证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校计划购买篮球、排球共20个,购买2个篮球,3个排球,共需花费190元;购买3个篮球的费用与购买5个排球的费用相同。
(1)篮球和排球的单价各是多少元?
(2)若购买篮球不少于8个,所需费用总额不超过800元.请你求出满足要求的所有购买方案,并直接写出其中最省钱的购买方案
-
科目: 来源: 题型:
查看答案和解析>>【题目】2018年3月,某市教育主管部门在初中生中开展了“文明礼仪知识竞赛”活动,活动结束后,随机抽取了部分同学的成绩(x均为整数,总分100分),绘制了如下尚不完整的统计图表.
调查结果统计表
组别
成绩分组(单位:分)
频数
频率
A
80≤x<85
50
0.1
B
85≤x<90
75
C
90≤x<95
150
c
D
95≤x≤100
a
合计
b
1
根据以上信息解答下列问题:
(1)统计表中,a=_____,b=_____,c=_____;
(2)扇形统计图中,m的值为_____,“C”所对应的圆心角的度数是_____;
(3)若参加本次竞赛的同学共有5000人,请你估计成绩在95分及以上的学生大约有多少人?

-
科目: 来源: 题型:
查看答案和解析>>【题目】小赵和小王交流暑假中的活动,小赵说:“我们一家外出旅行了一个星期,这7天的日期数之和是84天,你知道我们几号出去的么?”小王说“我暑假去舅舅家住了7天,日历数再加月份数也是84,你能猜出我是几月几号回的家?试试看列出方程,解决小赵、小王的问题.(提示:7月1日﹣9月1日暑假)

相关试题

