【题目】在△ABC中,AB=AC,∠BAC=150°,点A到BC的距离为1,与AB重合的一条射线AP,从AB开始,以每秒15°的速度绕点A逆时针匀速旋转,到达AC后立即以相同的速度返回AB,到达后立即重复上述旋转过程,设AP与BC边的交点为M,旋转2019秒时,BM= , CM= . 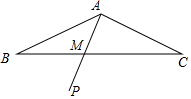
参考答案:
【答案】2;2+2 ![]()
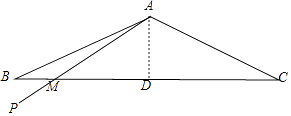
【解析】解:过A作AD⊥BC于D,则AD=1, ∵150=10×15,即AP从AB开始,绕点A逆时针匀速旋转10秒到达AC后再经过10秒返回AB,
而2019=100×20+19=100×20+10+9,
∴当旋转2019秒时,AP从AB绕点A逆时针匀速旋转了9秒,
∴此时CAP=15°×9=135°,
∴∠BAP=150°﹣135°=15°,
∵AB=AC,
∴BD=CD,∠B=∠C= ![]() (180°﹣150°)=15°,
(180°﹣150°)=15°,
∴AM=BM,∠AMD=∠B+∠BAP=30°,
∴BM=AM=2AD=2,MD= ![]() ,
,
∴CD=BD=2+ ![]() ,
,
∴CM=2+2 ![]() ,
,
所以答案是:2,2+2 ![]() .
.
【考点精析】掌握等腰三角形的性质和旋转的性质是解答本题的根本,需要知道等腰三角形的两个底角相等(简称:等边对等角);①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知矩形ABCD中,E是AD上的一点,F是AB上的一点,EF⊥EC,且EF=EC,DE=4cm,矩形ABCD的周长为32cm,求AE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1)所示,E为矩形ABCD的边AD上一点,动点P,Q同时从点B出发,点P沿折线BE﹣ED﹣DC运动到点C时停止,点Q沿BC运动到点C时停止,它们运动的速度都是1cm/秒.设P、Q同时出发t秒时,△BPQ的面积为ycm2 . 已知y与t的函数关系图象如图(2)(曲线OM为抛物线的一部分),则下列结论:①AD=BE=5;②
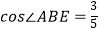 ;③当0<t≤5时,
;③当0<t≤5时, 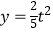 ;④当
;④当 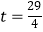 秒时,△ABE∽△QBP;其中正确的结论是( )
秒时,△ABE∽△QBP;其中正确的结论是( )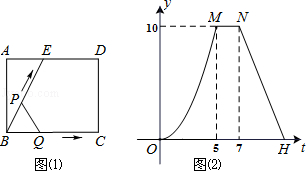
A.①②③
B.②③
C.①③④
D.②④ -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)在如图所示的数轴上,把数﹣2,
 ,4,﹣
,4,﹣ ,2.5表示出来,并用“<“将它们连接起来;
,2.5表示出来,并用“<“将它们连接起来;(2)假如在原点处放立一挡板(厚度不计),有甲、乙两个小球(忽略球的大小,可看作一点),小球甲从表示数﹣2的点处出发,以1个单位长度/秒的速度沿数轴向左运动;同时小球乙从表示数4的点处出发,以2个单位长度/秒的速度沿数轴向左运动,在碰到挡板后即刻按原来的速度向相反的方向运动,设运动的时间为t(秒).
请从A,B两题中任选一题作答.
A.当t=3时,求甲、乙两小球之间的距离.
B.用含t的代数式表示甲、乙两小球之间的距离.
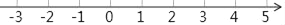
-
科目: 来源: 题型:
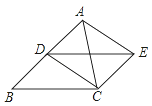
查看答案和解析>>【题目】已知,如图,点D是△ABC的边AB的中点,四边形BCED是平行四边形,
(1)求证:四边形ADCE是平行四边形;
(2)当△ABC满足什么条件时,平行四边形ADCE是矩形?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知凸四边形ABCD中,∠A=∠C=90°.
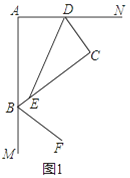
(1)如图1,若DE平分∠ADC,BF平分∠ABC的邻补角,判断DE与BF位置关系并证明.
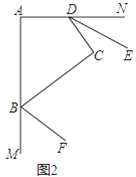
(2)如图2,若BF、DE分别平分∠ABC、∠ADC的邻补角,判断DE与BF位置关系并证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,放置的一副三角尺,将含45°角的三角尺斜边中点O为旋转中心,逆时针旋转30°得到如图2,连接OB、OD、AD.
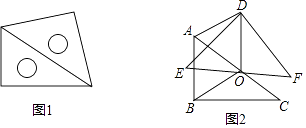
(1)求证:△AOB≌△AOD;
(2)试判定四边形ABOD是什么四边形,并说明理由.
相关试题

