【题目】把三根长为3cm、4cm和5cm的细木棒首尾相连,能搭成一个直角三角形.
(1)如果把这三根细木棒的长度分别扩大为原来的a倍(a>1),那么所得的三根细木棒能不能搭成一个直角三角形, 为什么?
(2)如果把这三根细木棒的长度分别延长x cm(x>0),那么所得的三根细木棒还能搭成一个三角形吗?为什么?如果能,请判断这个三角形的形状(锐角三角形、直角三角形还是钝角三角形),并说明理由.
参考答案:
【答案】(1)能搭成直角三角形;理由见解析;(2)能搭成一个三角形,且为锐角三角形. 理由见解析.
【解析】
(1)利用勾股定理的逆定理,即可得到结论;
(2)根据三角形的三边关系,即可判断等搭成一个三角形,由三角形两短边的平方和大于最长边的平方,可判断是锐角三角形,即可得到结论.
解:(1)把这三根细木棒的长度分别扩大为原来的a倍(a>1),
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴边长扩大为原来的a倍,仍能搭成一个直角三角形;
(2)把这三根细木棒的长度分别延长x cm,
∵(3+x)+(4+x)=7+2x,
∵x>0,
∴7+2x>5+x,
∴(3+x)+(4+x)>5+x;
∴以(3+x)、(4+x)、(5+x)为边,能搭成一个三角形;
∵![]() ,
,![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴这个三角形为锐角三角形.
-
科目: 来源: 题型:
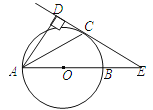
查看答案和解析>>【题目】如图,已知AB是⊙O的直径,锐角∠DAB的平分线AC交⊙O于点C,作CD⊥AD,垂足为D,直线CD与AB的延长线交于点E.
(1)求证:直线CD为⊙O的切线;
(2)当AB=2BE,且CE=时,求AD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】作图与探究:
如图,△ABC中,AB=AC.

(1)作图:①画线段BC的垂直平分线l,设l与BC边交于点H;
②在射线HA上画点D,使AD=AB,连接BD. (不写作法,保留作图痕迹)
(2)探究:∠D与∠C有怎样的数量关系? 并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某超市销售一种商品,成本每千克40元,规定每千克售价不低于成本,且不高于80元,经市场调查,每天的销售量y(千克)与每千克售价x(元)满足一次函数关系,部分数据如下表:
售价x(元/千克)
50
60
70
销售量y(千克)
100
80
60
(1)求y与x之间的函数表达式;
(2)设商品每天的总利润为W(元),则当售价x定为多少元时,厂商每天能获得最大利润?最大利润是多少?
(3)如果超市要获得每天不低于1350元的利润,且符合超市自己的规定,那么该商品每千克售价的取值范围是多少?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2017贵州省遵义市)如图,抛物线
 (a<0,a、b为常数)与x轴交于A、C两点,与y轴交于B点,直线AB的函数关系式为
(a<0,a、b为常数)与x轴交于A、C两点,与y轴交于B点,直线AB的函数关系式为 .
.(1)求该抛物线的函数关系式与C点坐标;
(2)已知点M(m,0)是线段OA上的一个动点,过点M作x轴的垂线l分别与直线AB和抛物线交于D、E两点,当m为何值时,△BDE恰好是以DE为底边的等腰三角形?
(3)在(2)问条件下,当△BDE恰好是以DE为底边的等腰三角形时,动点M相应位置记为点M′,将OM′绕原点O顺时针旋转得到ON(旋转角在0°到90°之间);
①探究:线段OB上是否存在定点P(P不与O、B重合),无论ON如何旋转,
 始终保持不变,若存在,试求出P点坐标;若不存在,请说明理由;
始终保持不变,若存在,试求出P点坐标;若不存在,请说明理由;②试求出此旋转过程中,(NA+
 NB)的最小值.
NB)的最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1) 观察被开方数a的小数点与算术平方根
 的小数点的移动规律:
的小数点的移动规律:a
0.0001
0.01
1
100
10000

0.01
x
1
y
100
填空:x= _______, y=______.
(2)根据你发现的规律填空:
①已知
 ≈1.414,则
≈1.414,则 =________,
=________, =_______;
=_______;②
 = 0.274,记
= 0.274,记 的整数部分为x,则
的整数部分为x,则 =___________.
=___________. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在梯形ABCD中,AB∥CD,∠D=90°,AD=CD=2,点E在边AD上(不与点A、D重合),∠CEB=45°,EB与对角线AC相交于点F,设DE=x.
(1)用含x的代数式表示线段CF的长;
(2)如果把△CAE的周长记作C△CAE,△BAF的周长记作C△BAF,设
 =y,求y关于x的函数关系式,并写出它的定义域;
=y,求y关于x的函数关系式,并写出它的定义域;(3)当∠ABE的正切值是
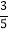 时,求AB的长.
时,求AB的长.
相关试题

