【题目】已知二次函数y=ax2+bx+c的图象上部分点的横坐标x与纵坐标y的对应值如下表:

那么关于它的图象,下列判断正确的是( )
A. 开口向上 B. 与x轴的另一个交点是(3,0)
C. 与y轴交于负半轴 D. 在直线x=1的左侧部分是下降的
参考答案:
【答案】B
【解析】A、由表格知,抛物线的顶点坐标是(1,4).故设抛物线解析式为y=a(x﹣1)2+4.
将(﹣1,0)代入,得
a(﹣1﹣1)2+4=0,
解得a=﹣2.
∵a=﹣2<0,
∴抛物线的开口方向向下,
故本选项错误;
B、抛物线与x轴的一个交点为(﹣1,0),对称轴是x=1,则抛物线与x轴的另一个交点是(3,0),故本选项正确;
C、由表格知,抛物线与y轴的交点坐标是(0,3),即与y轴交于正半轴,故本选项错误;
D、抛物线开口方向向下,对称轴为x=1,则在直线x=1的左侧部分是上升的,故本选项错误;
故选:B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于
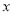 的一元二次方程
的一元二次方程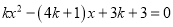 (
(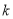 是整数).
是整数).⑴.求证:方程有两个不相等的实数根;
⑵.若方程的两个实数根分别为
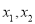 (其中
(其中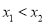 ),设
),设 ,判断
,判断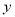 是否为变量
是否为变量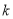 的函数?如果是,请写出函数表达式;若不是,请说明理由.
的函数?如果是,请写出函数表达式;若不是,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】“立定跳远”是我市初中毕业生体育测试项目之一.测试时,记录下学生立定跳远的成绩,然后按照评分标准转化为相应的分数,满分10分.其中男生立定跳远的评分标准如下:注:成绩栏里的每个范围,含最低值,不含最高值.
成绩(米)
…
1.80~1.86
1.86~1.94
1.94~2.02
2.02~2.18
2.18~2.34
2.34~
得分(分)
…
5
6
7
8
9
10
某校九年级有480名男生参加立定跳远测试,现从中随机抽取10名男生测试成绩(单位:分)如下:
1.96 2.38 2.56 2.04 2.34 2.17 2.60 2.26 1.87 2.32
请完成下列问题:
(1)求这10名男生立定跳远成绩的极差和平均数;
(2)求这10名男生立定跳远得分的中位数和众数;
(3)如果将9分(含9分)以上定为“优秀”,请你估计这480名男生中得优秀的人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】自学下面材料后,解答问题。
分母中含有未知数的不等式叫分式不等式。如:
 <0等。那么如何求出它们的解集呢?
<0等。那么如何求出它们的解集呢?根据我们学过的有理数除法法则可知:两数相除,同号得正,异号得负。其字母表达式为:
若a>0,b>0,则
 >0;若a<0,b<0,则
>0;若a<0,b<0,则 >0;
>0;若a>0,b<0,则
 <0;若a<0,b>0,则
<0;若a<0,b>0,则 <0.
<0.反之:若
 >0,则
>0,则 或
或 ,
,(1)若
 <0,则___或___.
<0,则___或___.(2)根据上述规律,求不等式
 >0的解集.
>0的解集. -
科目: 来源: 题型:
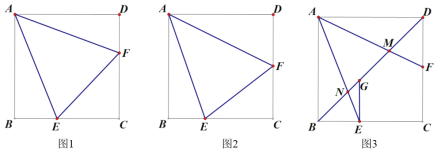
查看答案和解析>>【题目】已知正方形 ABCD,E 在线段 BC 上,F 在线段 CD 上.
(1)如图 1,连接 EF,若EAF =45,求证:BE+DF=EF;
(2)如图 2,连接 EF,若DAE=AEF ,且 2BE=CE,求
 的值;
的值;(3)如图 3,连接 BD,线段 AE、AF 分别交 BD 于点 N、M.已知GEB=90 ,DM=MG=4,NG=1,请直接写出线段AF 的长度.
-
科目: 来源: 题型:
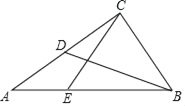
查看答案和解析>>【题目】已知:如图,在Rt△ABC中,∠ACB=90°,BC=
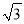 ,cot∠ABC=
,cot∠ABC=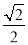 ,点D是AC的中点.
,点D是AC的中点.(1)求线段BD的长;
(2)点E在边AB上,且CE=CB,求△ACE的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】学校准备购进一批甲、乙两种办公桌若干张,并且每买
 张办公桌必须买两把椅子,椅子每把
张办公桌必须买两把椅子,椅子每把 元.若学校购买
元.若学校购买 张甲种办公桌和
张甲种办公桌和 张乙种办公桌共花费
张乙种办公桌共花费 元,购买
元,购买 张甲种办公桌比购买
张甲种办公桌比购买 张乙种办公桌多花费
张乙种办公桌多花费 元。
元。(1)求甲、乙两种办公桌每张各多少元?
(2)若学校准备用不超过
 元购买甲、乙两种办公桌共
元购买甲、乙两种办公桌共 张,且甲种办公桌数量不多于乙种办公桌数量的
张,且甲种办公桌数量不多于乙种办公桌数量的 倍,请求出有哪几种购买方案?
倍,请求出有哪几种购买方案?
相关试题

