Question

【题目】在平面直角坐标系xOy中，点P是抛物线：y=x2上的动点（点在第一象限内）．连接 OP，过点0作OP的垂线交抛物线于另一点Q．连接PQ，交y轴于点M．作PA丄x轴于点A，QB丄x轴于点B．设点P的横坐标为m．

（1）如图1，当m= 时，
①求线段OP的长和tan∠POM的值；
②在y轴上找一点C，使△OCQ是以OQ为腰的等腰三角形，求点C的坐标；
（2）如图2，连接AM、BM，分别与OP、OQ相交于点D、E．
①用含m的代数式表示点Q的坐标；
②求证：四边形ODME是矩形．

Answer 1

【答案】
（1）

解：①∵把x= 代入 y=x2，得 y=2，

∴P（ ，2），

∴OP=

∵PA丄x轴，

∴PA∥MO．

∴tan∠P0M=tan∠0PA= = ．

②设 Q（n，n2），

∵tan∠QOB=tan∠POM，

∴ ．

∴n=-

∴Q（- ， ），

∴OQ= ．

当OQ=OC时，则C1（0， ），C2（0，- ）；

当OQ=CQ时，则C3（0，1）；

当CQ=CO时，OQ为底，不合题意．

综上所述，当△OCQ是以OQ为腰的等腰三角形时，所求点C坐标为：C1（0， ），C2（0，- ），C3（0，1）

（2）

解：方法一：

①设 Q（n，n2），

∵△APO∽△BOQ，

∴

∴ ，得n=- ，

∴Q（- ， ）．

②设直线PQ的解析式为：y=kx+b，把P（m，m2）、Q（- ， ）代入，得：

，

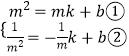①﹣②得：m2﹣ =（m+ ）k，

解得：k=m﹣ ③，

把③代入①，得：b=1，

∴M（0，1）

∵ ，∠QBO=∠MOA=90°，

∴△QBO∽△MOA

∴∠MAO=∠QOB，

∴QO∥MA

同理可证：EM∥OD

又∵∠EOD=90°，

∴四边形ODME是矩形．

方法二：

①OP⊥OQ，∴KOP×KOQ=﹣1，

∵KOP= = ，KOQ=﹣ ，

∴lOQ：y=﹣ x，y=x2

∴x1=0（舍），x2=﹣ ，

∴Q（﹣ ， ），

设点C（0，t），O（0，0），

∵△OCQ是以OQ为腰的等腰三角形．

∴OQ=OC或QO=QC，

∴（0+ ）2+（0﹣ ）2=（0﹣0）2+（0﹣t）2，∴t=± ，

∴（0+ ）2+（0﹣ ）2=（﹣ ﹣0）2+（ ﹣t）2，∴t=1，

∴C1（0， ），C2（0，﹣ ），C3（0，1），

∵Px=m，∴PY=m2，∴KOP=m，

又OQ⊥OP，∴KOP×KOQ=﹣1，∴KOQ=﹣ ，

∴lOQ：y=﹣ x，

∵y=x2，

∴Q（﹣ ， ），P（m，m2），

∴lPQ：y=（m﹣ ）x+1，

即M（0，1），又A（m，0），B（﹣ ，0），O（0，0），

∴KAM= =﹣ ，∵KOQ=﹣ ，KAM=KOQ，∴AM∥OQ，

∴KBM= =m，∵KOP=m，∴KBM=KOP，∴BM∥OP，

∴四边形ODME是平行四边形，又OP⊥OQ，

∴四边形ODME为矩形．

【解析】方法一：（1）①已知m的值，代入抛物线的解析式中可求出点P的坐标；由此确定PA、OA的长，通过解直角三角形易得出结论．②题干要求△OCQ是以OQ为腰的等腰三角形，所以分QO=OC、QC=QO、CQ=CO三种情况来判断：QO=QC时，Q在线段OC的垂直平分线上，Q、O的纵坐标已知，C点坐标即可确定；QO=OC时，先求出OQ的长，那么C点坐标可确定；
CQ=CO时，OQ为底，不合题意．（2）①由∠QOP=90°，易求得△QBO∽△MOA，通过相关的比例线段来表示出点Q的坐标；②在四边形ODME中，已知了一个直角，只需判定该四边形是平行四边形即可，那么可通过证明两组对边平行来得证．方法二：（1）略．（2）利用黄金法则二求出直线OQ的斜率与抛物线联立求出Q点坐标，再利用黄金法则四求出C点坐标3分别求出点M，A，O，B坐标，利用斜率相等，证明MA‖OQ，BM‖OP，从而得出四边形ODME是平行四边形，再利用OP⊥OQ证明矩形．