【题目】如图,在△ABC中,AB=AC,以AC边为直径作⊙O交BC边于点D,过点D作DE⊥AB于点E,ED、AC的延长线交于点F. 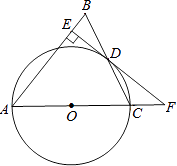
(1)求证:EF是⊙O的切线;
(2)若EB= ![]() ,且sin∠CFD=
,且sin∠CFD= ![]() ,求⊙O的半径与线段AE的长.
,求⊙O的半径与线段AE的长.
参考答案:
【答案】
(1)证明:连结OD,如图,
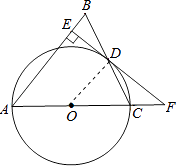
∵AB=AC,
∴∠B=∠ACD,
∵OC=OD,
∴∠ODC=∠OCD,
∴∠B=∠ODC,
∴OD∥AB,
∵DE⊥AB,
∴OD⊥EF,
∴EF是⊙O的切线
(2)解:在Rt△ODF,sin∠OFD= ![]() =
= ![]() ,
,
设OD=3x,则OF=5x,
∴AB=AC=6x,AF=8x,
在Rt△AEF中,∵sin∠AFE= ![]() =
= ![]() ,
,
∴AE= ![]() 8x=
8x= ![]() x,
x,
∵BE=AB﹣AE=6x﹣ ![]() x=
x= ![]() x,
x,
∴ ![]() x=
x= ![]() ,解得x=
,解得x= ![]() ,
,
∴AE= ![]()
![]() =6,
=6,
OD=3 ![]() =
= ![]() ,
,
即⊙O的半径长为 ![]() .
.
【解析】(1)连结OD,如图,由AB=AC得到∠B=∠ACD,由OC=OD得到∠ODC=∠OCD,则∠B=∠ODC,于是可判断OD∥AB,然后利用DE⊥AB得到OD⊥EF,然后根据切线的判定定理得到结论;(2)在Rt△ODF利用正弦的定义得到sin∠OFD= ![]() =
= ![]() ,则可设OD=3x,OF=5x,所以AB=AC=6x,AF=8x,在Rt△AEF中由于sin∠AFE=
,则可设OD=3x,OF=5x,所以AB=AC=6x,AF=8x,在Rt△AEF中由于sin∠AFE= ![]() =
= ![]() ,可得到AE=
,可得到AE= ![]() x,接着表示出BE得到
x,接着表示出BE得到 ![]() x=
x= ![]() ,解得x=
,解得x= ![]() ,于是可得到AE和OD的长.
,于是可得到AE和OD的长.
【考点精析】掌握切线的判定定理是解答本题的根本,需要知道切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,下列能判定AB∥CD的条件有( )个.
(1)∠B+∠BCD=180°;(2)∠1=∠2;(3)∠3=∠4;(4)∠B=∠5.

A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的对角线AC,BD相交于点O,延长CB至点F,使CF=CA,连接AF,∠ACF的平分线分别交AF,AB,BD于点E,N,M,连接EO,已知BD=
 .
.(1)求正方形ABCD的边长;
(2)求OE的长;
(3)①求证:CN=AF;
②直接写出四边形AFBO的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD中,AB=3cm,BC=5cm,∠B=60°,G是CD的中点,E是边AD上的动点,EG的延长线与BC的延长线交于点F,连接CE,DF.
(1)求证:四边形CEDF是平行四边形;
(2)①AE为何值时四边形CEDF是矩形?为什么?
②AE为何值时四边形CEDF是菱形?为什么?

-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人在一段长为1200m的笔直路上匀速跑步,甲、乙的速度分别为4m/s和6m/s,起跑前乙在起点,甲在乙前面100m处.若同时起跑,甲、乙两人在从起跑至其中一人先到达终点的过程中,他们之间的距离y(m)与时间t(s)的函数图像如图所示.则t1=________s,y2=________m.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某生物兴趣小组在四天的实验研究中发现:骆驼的体温会随外部环境温度的变化而变化,而且在这四天中每昼夜的体温变化情况相同.他们将一头骆驼前两昼夜的体温变化情况绘制成下图.请根据图像回答问题:
(1)第一天中,在什么时间范围内这头骆驼的体温是上升的?它的体温从最低上升到最高需要多少时间?
(2)第三天12时这头骆驼的体温约是多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,反比例函数y=
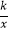 与一次函数y=ax+b的图象交于点A(2,2)、B(
与一次函数y=ax+b的图象交于点A(2,2)、B(  ,n).
,n). 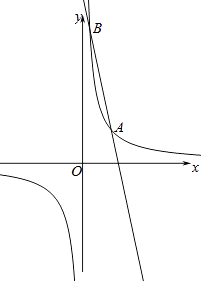
(1)求这两个函数解析式;
(2)将一次函数y=ax+b的图象沿y轴向下平移m个单位,使平移后的图象与反比例函数y=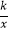 的图象有且只有一个交点,求m的值.
的图象有且只有一个交点,求m的值.
相关试题

