【题目】如图,平行四边形ABCD中,AB=3cm,BC=5cm,∠B=60°,G是CD的中点,E是边AD上的动点,EG的延长线与BC的延长线交于点F,连接CE,DF.
(1)求证:四边形CEDF是平行四边形;
(2)①AE为何值时四边形CEDF是矩形?为什么?
②AE为何值时四边形CEDF是菱形?为什么?

参考答案:
【答案】见解析
【解析】试题分析: (1)证△CFG≌△EDG,推出FG=EG,根据平行四边形的判定推出即可,(2)①求出△MBA≌△EDC,推出∠CED=∠AMB=90°,根据矩形的判定推出即可,②求出△CDE是等边三角形,推出CE=DE,根据菱形的判定推出即可.
试题解析:(1)证明:∵四边形ABCD是平行四边形,∴CF∥ED,∴∠FCG=∠EDG,∵G是CD的中点,∴CG=DG,在△FCG和△EDG中,
 ,
,
∴△FCG≌△EDG(ASA),
∴FG=EG,
∵CG=DG,
∴四边形CEDF是平行四边形,
(2)① 当AE=3.5时,平行四边形CEDF是矩形,理由是:过A作AM⊥BC于M,
∵∠B=60°,AB=3,∴BM=1.5,
∵四边形ABCD是平行四边形,
∴∠CDA=∠B=60°,DC=AB=3,BC=AD=5,
∵AE=3.5,
∴DE=1.5=BM,
在△MBA和△EDC中,
 ,
,
∴△MBA≌△EDC(SAS),
∴∠CED=∠AMB=90°,
∵四边形CEDF是平行四边形,
∴四边形CEDF是矩形,故答案为:3.5,
②当AE=2时,四边形CEDF是菱形,理由是:
∵AD=5,AE=2,
∴DE=3,
∵CD=3,∠CDE=60°,
∴△CDE是等边三角形,
∴CE=DE,
∵四边形CEDF是平行四边形,
∴四边形CEDF是菱形,故答案为:2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E是正方形ABCD对角线AC上一点,EF⊥AB,EG⊥BC,垂足分别为F,G,若正方形ABCD的周长是40cm.
(1)求证:四边形BFEG是矩形;
(2)求四边形EFBG的周长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,下列能判定AB∥CD的条件有( )个.
(1)∠B+∠BCD=180°;(2)∠1=∠2;(3)∠3=∠4;(4)∠B=∠5.

A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的对角线AC,BD相交于点O,延长CB至点F,使CF=CA,连接AF,∠ACF的平分线分别交AF,AB,BD于点E,N,M,连接EO,已知BD=
 .
.(1)求正方形ABCD的边长;
(2)求OE的长;
(3)①求证:CN=AF;
②直接写出四边形AFBO的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,以AC边为直径作⊙O交BC边于点D,过点D作DE⊥AB于点E,ED、AC的延长线交于点F.
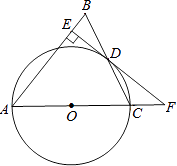
(1)求证:EF是⊙O的切线;
(2)若EB= ,且sin∠CFD=
,且sin∠CFD= 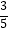 ,求⊙O的半径与线段AE的长.
,求⊙O的半径与线段AE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人在一段长为1200m的笔直路上匀速跑步,甲、乙的速度分别为4m/s和6m/s,起跑前乙在起点,甲在乙前面100m处.若同时起跑,甲、乙两人在从起跑至其中一人先到达终点的过程中,他们之间的距离y(m)与时间t(s)的函数图像如图所示.则t1=________s,y2=________m.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某生物兴趣小组在四天的实验研究中发现:骆驼的体温会随外部环境温度的变化而变化,而且在这四天中每昼夜的体温变化情况相同.他们将一头骆驼前两昼夜的体温变化情况绘制成下图.请根据图像回答问题:
(1)第一天中,在什么时间范围内这头骆驼的体温是上升的?它的体温从最低上升到最高需要多少时间?
(2)第三天12时这头骆驼的体温约是多少?

相关试题

