【题目】如图,正方形ABCD与正方形EFGH是位似形,已知A(0,5),D(0,3),E(0,1),H(0,4),则位似中心的坐标是 . 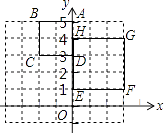
参考答案:
【答案】(0,![]() ),(﹣6,7)
),(﹣6,7)
【解析】解:设当B与F是对应点,设直线BF的解析式为:y=kx+b,
则 ![]() ,
,
解得: 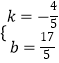 ,
,
故直线BF的解析式为:y=﹣ ![]() x+
x+ ![]() ,
,
则x=0时,y= ![]() ,
,
即位似中心是:(0, ![]() ),
),
设当C与E是对应点,设直线CE的解析式为:y=ax+c,
则 ![]() ,
,
解得: ![]() ,
,
故直线CE的解析式为:y=﹣x+1,
设直线DF的解析式为:y=dx+e,
则 ![]() ,
,
解得: 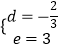 ,
,
故直线DF的解析式为:y=﹣ ![]() x+3,
x+3,
则  ,
,
解得: ![]()
即位似中心是:(﹣6,7),
综上所述:所述位似中心为:(0, ![]() ),(﹣6,7).
),(﹣6,7).
所以答案是:(0, ![]() ),(﹣6,7).
),(﹣6,7).
【考点精析】通过灵活运用位似变换,掌握它们具有相似图形的性质外还有图形的位置关系(每组对应点所在的直线都经过同一个点—位似中心)即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中有两点A(4,0)、B(0,2),如果点C在x轴上(C与A不重合),当点C的坐标为或时,使得由点B、O、C组成的三角形与△AOB相似(至少找出两个满足条件的点的坐标).
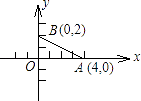
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于一个图形,通过两种不同的方法计算它的面积,可以得到一个数学等式,例如图1可以得到(a+b)2=a2+2ab+b2,请解答下列问题:
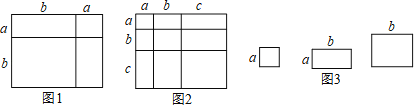
(1)写出图2中所表示的数学等式 。
(2)根据整式乘法的运算法则,通过计算验证上述等式。
(3)利用(1)中得到的结论,解决下面的问题:
若a+b+c=10,ab+ac+bc=35,则a2+b2+c2= .
(4)小明同学用图3中x张边长为a的正方形,y张边长为b的正方形z张边长分别为a、b的长方形纸片拼出一个面积为(5a+7b)(9a+4b)长方形,则x+y+z= 。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,△ABC中,∠B=90°,AB=6cm,BC=8cm.
(1)点P从点A开始沿AB边向B以1cm/s的速度移动,点Q从B点开始沿BC边向点C以2cm/s的速度移动.如果P,Q分别从A,B同时出发,经过几秒,使△PBQ的面积等于8cm2?
(2)点P从点A开始沿AB边向B以1cm/s的速度移动,点Q从B点开始沿BC边向点C以2cm/s的速度移动.如果P,Q分别从A,B同时出发,线段PQ能否将△ABC分成面积相等的两部分?若能,求出运动时间;若不能说明理由.
(3)若P点沿射线AB方向从A点出发以1cm/s的速度移动,点Q沿射线CB方向从C点出发以2cm/s的速度移动,P,Q同时出发,问几秒后,△PBQ的面积为1?

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,AD∥BE,∠B=∠D,直线AB与DC平行吗?说明理由(请在下面的解答过程的空格内填空或在括号内填写理由)。
解:直线AB与DC平行.理由如下:
∵ AD∥BE (已知 )
∴ ∠D = ∠DCE ( )
又∵∠B = ∠D ( )
∴∠B = ∠_____ (等量代换)
∴ AB∥DC ( )
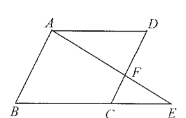
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学学生会为了解该校学生喜欢球类活动的情况,随机抽取了若干名学生进行问卷调查(要求每位学生只能填写一种自己喜欢的球类),并将调查的结果绘制成如图所示的两幅不完整的统计图.(
 把圆分成面积相等的两部分)请根据图中提供的信息,解答下列问题:
把圆分成面积相等的两部分)请根据图中提供的信息,解答下列问题: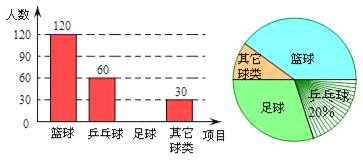
(1)参加调查的人数共有_______人;在扇形图中,表示“其它球类”的扇形的圆心角为______度;
(2)将条形图补充完整;
(3)若该校有
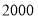 名学生,估计喜欢“乒乓球”的学生共有多少人?
名学生,估计喜欢“乒乓球”的学生共有多少人? -
科目: 来源: 题型:
查看答案和解析>>【题目】福建省教育厅日前发布文件,从2019年开始,体育成绩将按一定的原始分计入中考总分。某校为适应新的中考要求,决定为体育组添置一批体育器材。学校准备在网上订购一批某品牌足球和跳绳,在查阅天猫网店后发现足球每个定价150元,跳绳每条定价30元.现有A、B两家网店均提供包邮服务,并提出了各自的优惠方案.
A网店:买一个足球送一条跳绳;
B网店:足球和跳绳都按定价的90%付款.
已知要购买足球40个,跳绳x条(x>40)
(1)若在A网店购买,需付款 元(用含x的代数式表示).
若在B网店购买,需付款 元(用含x的代数式表示).
(2)若x=100时,通过计算说明此时在哪家网店购买较为合算?
(3)当x=100时,你能给出一种更为省钱的购买方案吗?试写出你的购买方法,
并计算需付款多少元?
相关试题

