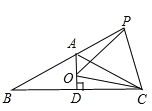
【题目】如图,在等腰三角形ABC中,AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC,下面的结论:①∠APO+∠DCO=30°;②△OPC是等边三角形;③AC=AO+AP;④![]() .其中所有正确结论的序号为 ( )
.其中所有正确结论的序号为 ( )
A.①②③ B.①②④ C.①③④ D.①②③④
参考答案:
【答案】D.
【解析】
试题解析:连接OB,
∵AB=AC,AD⊥BC,
∴BD=CD,∠BAD=![]() ∠BAC=
∠BAC=![]() ×120°=60°,
×120°=60°,
∴OB=OC,∠ABC=90°-∠BAD=30°,
∵OP=OC,
∴OB=OC=OP,
∴∠APO=∠ABO,∠DCO=∠DBO,
∴∠APO+∠DCO=∠ABO+∠DBO=∠ABD=30°;
故①正确;
∵∠APC+∠DCP+∠PBC=180°,
∴∠APC+∠DCP=150°,
∵∠APO+∠DCO=30°,
∴∠OPC+∠OCP=120°,
∴∠POC=180°-(∠OPC+∠OCP)=60°,
∵OP=OC,
∴△OPC是等边三角形;
故②正确;
在AC上截取AE=PA,
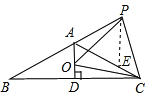
∵∠PAE=180°-∠BAC=60°,
∴△APE是等边三角形,
∴∠PEA=∠APE=60°,PE=PA,
∴∠APO+∠OPE=60°,
∵∠OPE+∠CPE=∠CPO=60°,
∴∠APO=∠CPE,
∵OP=CP,
在△OPA和△CPE中,
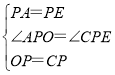
∴△OPA≌△CPE(SAS),
∴AO=CE,
∴AC=AE+CE=AO+AP;
故③正确;
过点C作CH⊥AB于H,
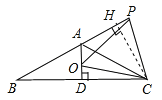
∵∠PAC=∠DAC=60°,AD⊥BC,
∴CH=CD,
∴S△ABC=![]() AB
AB![]() CH,
CH,
S四边形AOCP=S△ACP+S△AOC=![]() AP
AP![]() CH+
CH+![]() OA
OA![]() CD=
CD=![]() AP
AP![]() CH+
CH+![]() OA
OA![]() CH=
CH=![]() CH
CH![]() (AP+OA)=
(AP+OA)=![]() CH
CH ![]() AC,
AC,
∴S△ABC=S四边形AOCP;
故④正确.
故选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2+(m+3)x+m+1=0.求证:无论m取何值,原方程总有两个不相等的实数根.
-
科目: 来源: 题型:
查看答案和解析>>【题目】不等式2x-7<5-2x的正整数解的和是_________
-
科目: 来源: 题型:
查看答案和解析>>【题目】探究:如图,已知直线l1∥l2,直线l3和直线l1、l2交于点C和D,直线l3有一点P,
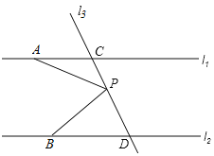
(1)若点P在C、D之间运动时,问∠PAC,∠APB,∠PBD之间的关系是否发生变化,并说明理由.
(2)若点P在C、D两点的外侧运动时(P点与点C、D不重合),试探索∠PAC,∠APB,∠PBD之间的关系又是如何?并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某件商品的标价是330元,按标价的八折销售可获利10%,则这种商品的进价为_________________________元。
-
科目: 来源: 题型:
查看答案和解析>>【题目】以下列长度线段为边,不能构成直角三角形的是( )
A. 7,24,25 B. 8,15,17 C. 9,40,41 D. 10,24,28
-
科目: 来源: 题型:
查看答案和解析>>【题目】若x是y的一个平方根,则y的算术平方根是( )
A. x B. -x C. ±x D. |x|
相关试题

