搜索
【题目】已知关于x的一元二次方程x2＋(m＋3)x＋m＋1＝0.求证：无论m取何值，原方程总有两个不相等的实数根．
参考答案：
【答案】详见解析
【解析】
表示出△,将△配方,进而判断△的正负性即可解题.
证明：∵Δ＝(m＋3)2－4(m＋1)＝(m＋1)2＋4，无论m取何值时，(m＋1)2＋4的值恒大于0，
∴原方程总有两个不相等的实数根．
-
科目： 来源： 题型：
查看答案和解析>>【题目】下面的计算正确的是（ ）
A.6a－5a=1
B.a＋2a2=2a3
C.－(a－b)= －a＋b
D.2(a＋b) =2a＋b -
科目： 来源： 题型：
查看答案和解析>>【题目】多项式2xy-3xy2+25的次数及最高次项的系数分别是（ ）
A.3，－3
B.2，－3
C.5，－3
D.2，3 -
科目： 来源： 题型：
查看答案和解析>>【题目】下列说法错误的是（ ）
A．有一组对边平行但不相等的四边形是梯形
B．有一个角是直角的梯形是直角梯形
C．等腰梯形的两底角相等
D．直角梯形的两条对角线不相等
-
科目： 来源： 题型：
查看答案和解析>>【题目】不等式2x-7<5-2x的正整数解的和是_________
-
科目： 来源： 题型：
查看答案和解析>>【题目】探究：如图，已知直线l1∥l2，直线l3和直线l1、l2交于点C和D，直线l3有一点P，
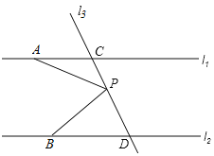
（1）若点P在C、D之间运动时，问∠PAC，∠APB，∠PBD之间的关系是否发生变化，并说明理由．
（2）若点P在C、D两点的外侧运动时（P点与点C、D不重合），试探索∠PAC，∠APB，∠PBD之间的关系又是如何？并说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在等腰三角形ABC中，AB=AC，∠BAC=120°，AD⊥BC于点D，点P是BA延长线上一点，点O是线段AD上一点，OP=OC，下面的结论:①∠APO+∠DCO=30°；②△OPC是等边三角形；③AC=AO+AP；④
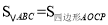．其中所有正确结论的序号为 ( )
A.①②③ B．①②④ C．①③④ D．①②③④
相关试题
