【题目】如图,扇形AOB中,半径OA=2,∠AOB=120°,C是 ![]() 的中点,连接AC、BC,则图中阴影部分面积是( )
的中点,连接AC、BC,则图中阴影部分面积是( ) 
A.![]() ﹣2
﹣2 ![]()
B.![]() ﹣2
﹣2 ![]()
C.![]() ﹣
﹣ ![]()
D.![]() ﹣
﹣ ![]()
参考答案:
【答案】A
【解析】解:连接OC,过O作OM⊥AC于M, 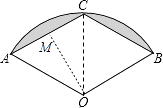
∵∠AOB=120°,C为弧AB中点,
∴∠AOC=∠BOC=60°,
∵OA=OC=OB=2,
∴△AOC、△BOC是等边三角形,
∴AC=BC=OA=2,AM=1,
∴△AOC的边AC上的高是 ![]() =
= ![]() ,
,
△BOC边BC上的高为 ![]() ,
,
∴阴影部分的面积是 ![]() ﹣
﹣ ![]() ×2×
×2× ![]() +
+ ![]() ﹣
﹣ ![]() ×2×
×2× ![]() =
= ![]() π﹣2
π﹣2 ![]() ,
,
故选:A.
【考点精析】利用扇形面积计算公式对题目进行判断即可得到答案,需要熟知在圆上,由两条半径和一段弧围成的图形叫做扇形;扇形面积S=π(R2-r2).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图①,△ABC是等边三角形,点D、E分别在边AB、BC上,且BD=BE,连接DE.
(1)求证:DE∥AC;
(2)将图①中的△BDE绕点B顺时针旋转,使得点A、D、E在同一条直线上,如图②,求∠AEC的度数;
(3)在(2)的条件下,如图③,连接CD,过点D作DM⊥BE于点M,在线段BM上取点N,使得∠DNE+∠DCE=180°.求证:EN﹣EC=2MN.

-
科目: 来源: 题型:
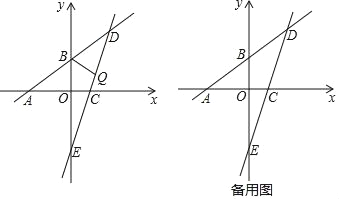
查看答案和解析>>【题目】已知:如图,一次函数
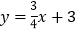 的图象分别与x轴、y轴相交于点A、B,且与经过点C(2,0)的一次函数y=kx+b的图象相交于点D,点D的横坐标为4,直线CD与y轴相交于点E.
的图象分别与x轴、y轴相交于点A、B,且与经过点C(2,0)的一次函数y=kx+b的图象相交于点D,点D的横坐标为4,直线CD与y轴相交于点E.(1)直线CD的函数表达式为 ;(直接写出结果)
(2)点Q为线段DE上的一个动点,连接BQ.
①若直线BQ将△BDE的面积分为1:2两部分,试求点Q的坐标;
②将△BQD沿着直线BQ翻折,使得点D恰好落在直线AB下方的坐标轴上,请直接写出点Q的坐标: .
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两名同学进行了6轮投篮比赛,两人的得分情况统计如下:
第1轮
第2轮
第3轮
第4轮
第5轮
第6轮
甲
10
14
12
18
16
20
乙
12
11
9
14
22
16
下列说法不正确的是( )
A.甲得分的极差小于乙得分的极差
B.甲得分的中位数大于乙得分的中位数
C.甲得分的平均数大于乙得分的平均数
D.乙的成绩比甲的成绩稳定 -
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a≠0)的图象如图,给出下列四个结论: ①4ac﹣b2<0;②4a+c<2b;③3b+2c<0;④m(am+b)+b<a(m≠﹣1),
其中正确结论的个数是( )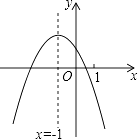
A.4个
B.3个
C.2个
D.1个 -
科目: 来源: 题型:
查看答案和解析>>【题目】为增强居民节约用电意识,某市对居民用电实行“阶梯收费”,具体收费标准见下表:

某居民五月份用电190千瓦时,缴纳电费90元.
(1)求x的值和超出部分电费单价;
(2)若该户居民六月份所缴电费不低于75元且不超过84元,求该户居民六月份的用电量范围.
-
科目: 来源: 题型:
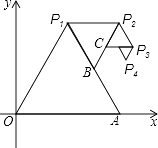
查看答案和解析>>【题目】如图,以O(0,0)、A(2,0)为顶点作正△OAP1 , 以点P1和线段P1A的中点B为顶点作正△P1BP2 , 再以点P2和线段P2B的中点C为顶点作△P2CP3 , …,如此继续下去,则第六个正三角形中,不在第五个正三角形上的顶点P6的坐标是 .
相关试题

