【题目】如图,点A、B、C分别是⊙O上的点,∠B=60°,AC=3,CD是⊙O的直径,P是CD延长线上的一点,且AP=AC.
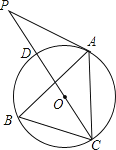
(1)求证:AP是⊙O的切线;
(2)求PD的长.
参考答案:
【答案】(1)见解析;(2)![]() .
.
【解析】
试题分析:(1)首先连接OA,由∠B=60°,利用圆周角定理,即可求得∠AOC的度数,又由OA=OC,即可求得∠OAC与∠OCA的度数,利用三角形外角的性质,求得∠AOP的度数,又由AP=AC,利用等边对等角,求得∠P,则可求得∠PAO=90°,则可证得AP是⊙O的切线;
(2)由CD是⊙O的直径,即可得∠DAC=90°,然后利用三角函数与等腰三角形的判定定理,即可求得PD的长.
(1)证明:连接OA.
∵∠B=60°,
∴∠AOC=2∠B=120°,
又∵OA=OC,
∴∠ACP=∠CAO=30°,
∴∠AOP=60°,
∵AP=AC,
∴∠P=∠ACP=30°,
∴∠OAP=90°,
∴OA⊥AP,
∴AP是⊙O的切线,
(2)解:连接AD.
∵CD是⊙O的直径,
∴∠CAD=90°,
∴AD=ACtan30°=3×![]() =
=![]() ,
,
∵∠ADC=∠B=60°,
∴∠PAD=∠ADC﹣∠P=60°﹣30°=30°,
∴∠P=∠PAD,
∴PD=AD=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列能平方差公式计算的式子是( )
A. (a﹣b)(b﹣a) B. (﹣x+1)(x﹣1)
C. (﹣a﹣1)(a+1) D. (﹣x﹣y)(﹣x+y)
-
科目: 来源: 题型:
查看答案和解析>>【题目】下表中是一次函数的自变量x与函数y的部分对应值.
x
﹣2
0
1
y
1
m
4
(1)求一次函数的表达式并求m的值.
(2)画出函数图象,结合图象思考:若y>0,则x的取值范围是 .(直接写出结论)
-
科目: 来源: 题型:
查看答案和解析>>【题目】在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示,现将△ABC平移,使点A变换为点A′,点B′、C′分别是B、C的对应点.

(1)请画出平移后的△A′B′C′,并求△A′B′C′的面积;
(2)若连接AA′,CC′,则这两条线段之间的关系是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(2a+3b,-2)和A'(-1,3a+b)关于y轴对称,则a+b的值为_______.
-
科目: 来源: 题型:
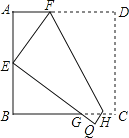
查看答案和解析>>【题目】如图,将边长为6cm的正方形ABCD折叠,使点D落在AB边的中点E处,折痕为FH,点C落在Q处,EQ与BC交于点G,则△EBG的周长是 cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个正方体的六个面上分别标有﹣1,﹣2,﹣3,﹣4,﹣5,﹣6中的一个数,各个面上所标数字都不相同,如图是这个正方体的三种放置方法,三个正方体下底面所标数字分别是a,b,c,则a+b+c+abc= .

相关试题

