【题目】骑自相车旅行越来越受到人们的喜爱,顺风车行经营的A型车2016年4月份销售总额为3.2万元,今年经过改造升级后A型车每辆销售比去年增加400元,若今年4月份与去年4月份卖出的A型车数量相同,则今年4月份A型车销售总额将比去年4月份销售总额增加25%.
(1)求今年4月份A型车每辆销售价多少元(用列方程的方法解答);
(2)该车行计划5月份新进一批A型车和B型车共50辆,且B型车的进货数量不超过A型车数量的两倍,应如何进货才能使这批车获利最多? A、B两种型号车的进货和销售价格如表:
A型车 | B型车 | |
进货价格(元/辆) | 1100 | 1400 |
销售价格(元/辆) | 今年的销售价格 | 2400 |
参考答案:
【答案】
(1)解:设去年A型车每辆x元,那么今年每辆(x+400)元,根据题意得:
![]() =
= ![]() ,
,
解得:x=1600,
经检验,x=1600是方程的解.
答:今年A型车每辆2000元
(2)解:设今年5月份进A型车m辆,则B型车(50﹣m)辆,获得的总利润为y元,
根据题意得:50﹣m≤2m
解得:m≥16 ![]() ,
,
∵y=(2000﹣1100)m+(2400﹣1400)(50﹣m)=﹣100m+50000,
∴y随m 的增大而减小,
∴当m=17时,可以获得最大利润.
答:进货方案是A型车17辆,B型车33辆
【解析】(1)设去年A型车每辆x元,那么今年每辆(x+400)元,根据今年4月份与去年4月份卖出的A型车数量相同,列方程求解即可;(2)设今年5月份进A型车m辆,则B型车(50﹣m)辆,获得的总利润为y元,先求出m的范围,构建一次函数,利用函数性质解决问题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算下列各题:
(1)
 -
- -
- +
+ ;
;(2)
 ×2×32-
×2×32-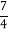 ÷(-1.75);
÷(-1.75);(3)-13×
 -0.34×
-0.34× +
+ ×(-13)-
×(-13)- ×0.34.
×0.34. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为一斜坡,其坡角为19.5°,紧挨着斜坡AB底部A处有一高楼,一数学活动小组量得斜坡长AB=15m,在坡顶B处测得楼顶D处的仰角为45°,其中测量员小刚的身高BC=1.7米,求楼高AD.
(参考数据:sin19.5°≈ ,tan19.5°≈
,tan19.5°≈  ,最终结果精确到0.1m).
,最终结果精确到0.1m).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,∠A=36°,BD、CE分别是∠ABC、∠BCD的角平分线,则图中的等腰三角形有( )

A. 5个 B. 4个 C. 3个 D. 2个
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料: 如图1,在平面直角坐标系xOy中,直线y1=ax+b与双曲线y2=
 交于A(1,3)和B(﹣3,﹣1)两点.
交于A(1,3)和B(﹣3,﹣1)两点.
观察图象可知:
①当x=﹣3或1时,y1=y2;
②当﹣3<x<0或x>1时,y1>y2 , 即通过观察函数的图象,可以得到不等式ax+b> 的解集.
的解集.
有这样一个问题:求不等式x3+4x2﹣x﹣4>0的解集.
某同学根据学习以上知识的经验,对求不等式x3+4x2﹣x﹣4>0的解集进行了探究.
下面是他的探究过程,请将(1)、(2)、(3)补充完整:
将不等式按条件进行转化:
当x=0时,原不等式不成立;
当x>0时,原不等式可以转化为x2+4x﹣1> ;
;
当x<0时,原不等式可以转化为x2+4x﹣1< ;
;
(1)构造函数,画出图象 设y3=x2+4x﹣1,y4= ,在同一坐标系中分别画出这两个函数的图象.
,在同一坐标系中分别画出这两个函数的图象.
双曲线y4= 如图2所示,请在此坐标系中画出抛物线y3=x2+4x﹣1;(不用列表)
如图2所示,请在此坐标系中画出抛物线y3=x2+4x﹣1;(不用列表)
(2)确定两个函数图象公共点的横坐标 观察所画两个函数的图象,猜想并通过代入函数解析式验证可知:满足y3=y4的所有x的值为;
(3)借助图象,写出解集 结合讨论结果,观察两个函数的图象可知:不等式x3+4x2﹣x﹣4>0的解集为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】小力在电脑上设计了一个有理数运算程序:输入a,加※键,再输入b,得到运算a※b=a2-b2-[2(a-1)-
 ]÷(a-b).
]÷(a-b).(1)求(-2)※
 的值;
的值;(2)小华在运用此程序计算时,屏幕显示“该程序无法操作”,你猜小华在输入数据时,可能出现什么情况?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,“回”字形的道路宽为1米,整个“回”字形的长为8米,宽为1米,一个人从入口点A沿着道路中央走到中点B,他共走了( )

A. 55米 B. 55.5米 C. 56米 D. 56.5米
相关试题

