【题目】如图,数轴上一动点![]() 从原点出发,在数轴上进行往返运动,运动情况如下表(注:表格中的
从原点出发,在数轴上进行往返运动,运动情况如下表(注:表格中的![]() 表示2到4之间的数).
表示2到4之间的数).
![]()
运动次数 | 运动方向 | 运动路程 | 数轴上对应的数 |
第1次 | _________ | 3 | -3 |
第2次 | 左 |
| _________ |
第3次 | _________ | _________ |
|
回答下列问题:
(1)完成表格;
(2)已知第4次运动的路程为![]() .
.
①此时数轴上对应的数是_________;
②若第4次运动后点![]() 恰好回到原点,则这4次运动的总路程是多少?
恰好回到原点,则这4次运动的总路程是多少?
参考答案:
【答案】(1)左 ,![]() , 右,
, 右, ![]() ;(2)①
;(2)①![]() 或
或![]() ;②32.
;②32.
【解析】
(1)根据始点与终点的数字符号确定第一次运动方向;第一次终点数字与第二次运动路程的差即第二次终点数字;根据第三次终点数字与第二次终点数字的差的符号确定运动方向和运动路程.
(2)①分向左或向右两种可能,根据![]() 确定第四次移动后最终在数轴上的对应数字;
确定第四次移动后最终在数轴上的对应数字;
②根据第四次运动后的对应数字确定![]() 的值,再计算总路程.
的值,再计算总路程.
解:(1)动点![]() 从原点
从原点![]() 运动到点-3,所以是向左运动;
运动到点-3,所以是向左运动;
再从点-3向左运动![]() ,故终点数字是
,故终点数字是![]() ;
;
∵![]() ,
,
∴![]() ,
,
∴第三次点![]() 是向右运动,运动路程是
是向右运动,运动路程是![]() ,
,
故答案为:左,![]() ,右,
,右,![]() .
.
(2)①向右运动时,![]() ;
;
向左运动时,![]() ,
,
故答案为![]() 或
或![]() ;
;
②当![]() 时,
时,![]() 或-0.5,不符合题意;
或-0.5,不符合题意;
当![]() 时,
时,![]() ,
,
![]()
![]() ,
,
所以这4次运动的总路程是32.
-
科目: 来源: 题型:
查看答案和解析>>【题目】张庄甲、乙两家草莓采摘园的草莓销售价格相同,“春节期间”,两家采摘园将推出优惠方案,甲园的优惠方案是:游客进园需购买门票,采摘的草莓六折优惠;乙园的优惠方案是:游客进园不需购买门票,采摘园的草莓超过一定数量后,超过部分打折优惠.优惠期间,某游客的草莓采摘量为
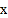 (千克),在甲园所需总费用为
(千克),在甲园所需总费用为 (元),在乙园所需总费用为
(元),在乙园所需总费用为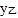 (元),
(元), 、
、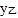 与
与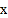 之间的函数关系如图所示,折线OAB表示
之间的函数关系如图所示,折线OAB表示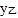 与
与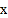 之间的函数关系.
之间的函数关系.
(1)甲采摘园的门票是 元,两个采摘园优惠前的草莓单价是每千克 元;
(2)当
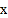 >10时,求
>10时,求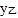 与
与 的函数表达式;
的函数表达式;(3)游客在“春节期间”采摘多少千克草莓时,甲、乙两家采摘园的总费用相同.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在矩形ABCD中,F是DC上一点,AE平分∠BAF交BC于点E,且DE⊥AF,垂足为点M,BE=3,AE=2
 ,则MF的长是 .
,则MF的长是 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是
①AD是∠BAC的平分线;②∠ADC=60°;③点D在AB的中垂线上;④S△DAC:S△ABC=1:3.

A.1 B.2 C.3 D.4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠AOB是平角,∠DOE=90°,OC平分∠DOB.
(1)若∠AOE=32°,求∠BOC的度数;
(2)若OD是∠AOC的角平分线,求∠AOE的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中,已知点A(﹣3,0)、B(0,4),对△OAB连续作旋转变换,依次得到△1、△2、△3、△4、…,△16的直角顶点的坐标为( )
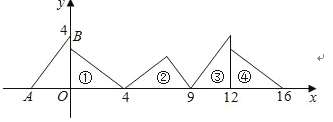

A. (60,0) B. (72,0) C. (67
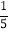 ,
,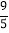 ) D. (79
) D. (79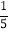 ,
,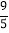 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知等腰△OPQ的顶点P的坐标为(4,3),O为坐标原点,腰长OP=5,点Q位于y轴正半轴上,则点Q的坐标为_____.
相关试题

