【题目】在数学活动课上,小明提出这样一个问题:∠B=∠C=90°,E是BC的中点,DE平分∠ADC,∠CED=35°,如图,则∠EAB是多少度?

参考答案:
【答案】35°.
【解析】
过点E作AD的垂线,垂足为F,根据∠DFE=∠C=90°,DE平分∠ADC,可证△DCE≌△DFE,可得∠DEC=∠DEF,EC=EF,又已知EC=EB,可得EF=EB,且∠B=∠EFA=90°,可证△AFE≌ABE,可知∠FEA=∠BEA,又∠DEC+∠DEF+∠FEA+∠BEA=180°,从而可得∠AED=90°再利用互余关系证明∠EAB=∠CED.
解:过点E作AD的垂线,垂足为F,
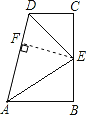
∵∠DFE=∠C=90°,DE平分∠ADC,DE=DE,
∴△DCE≌△DFE(AAS),
∴∠DEC=∠DEF,EC=EF,
又∵EC=EB,则EF=EB,且∠B=∠EFA=90°,AE=AE,
∴△AFE≌△ABE(HL),
∴∠FEA=∠BEA,
又∵∠DEC+∠DEF+∠FEA+∠BEA=180°,
∴∠AED=90°,
∴∠CED+∠BEA=90°,
又∠EAB+∠BEA=90°,
∴∠EAB=∠CED=35°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知菱形ABCD在平面直角坐标系的位置如图所示,A(1,1),B(6,1),AC=4
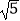 ,点P是对角线OAC上的一个动点,E(0,2),当△EPD周长最小时,点P的坐标为( )
,点P是对角线OAC上的一个动点,E(0,2),当△EPD周长最小时,点P的坐标为( ) 
A.(2,2)
B.(2,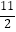 )
)
C.(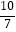 ,
,  )
)
D.( ,
, 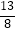 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,公园有一条“Z”字形道路ABCD,其中AB∥CD,在E,M,F处各有一个小石凳,E、F分别在AB、CD上,且BE=CF,M为BC的中点,请问三个小石凳是否在一条直线上?说出你推断的理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】含45°角的直角三角板如图放置在平面直角坐标系中,其中A(﹣2,0),B(0,1),则直线BC的解析式为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的长为2
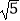 cm,对角线交于点O,以AB,AO为邻边做平行四边形AOCB,对角线交于点O,以AB、AO1为邻边做平行四边形AO1C1B,…,依此类推,则平行四边形AO6C6B的面积为cm2 .
cm,对角线交于点O,以AB,AO为邻边做平行四边形AOCB,对角线交于点O,以AB、AO1为邻边做平行四边形AO1C1B,…,依此类推,则平行四边形AO6C6B的面积为cm2 . 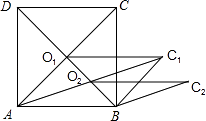
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,反比例函数y=
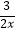 的图象上有一动点A,连接AO并延长交图象的另一支于点B,在第二象限内有一点C,满足AC=BC,当点A运动时,点C始终在函数y=
的图象上有一动点A,连接AO并延长交图象的另一支于点B,在第二象限内有一点C,满足AC=BC,当点A运动时,点C始终在函数y= 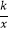 的图象上运动,tan∠CAB=2,则关于x的方程x2﹣5x+k=0的解为 .
的图象上运动,tan∠CAB=2,则关于x的方程x2﹣5x+k=0的解为 . 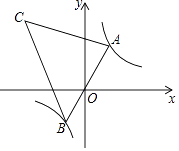
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,若一次函数
 的图象与x轴的交于点
的图象与x轴的交于点 ,与y轴交于点
,与y轴交于点 下列结论:①关于x的方程
下列结论:①关于x的方程 的解为
的解为 ;②
;② 随x的增大而减小;③关于x的方程
随x的增大而减小;③关于x的方程 的解为
的解为 ;④关于x的不等式
;④关于x的不等式 的解为
的解为 其中所有正确的为
其中所有正确的为


A. ①②③ B. ①③ C. ①②④ D. ②④
相关试题

