【题目】如图,四边形ABCD中,对角线AC与BD相交于点O,在①AB∥CD;②AO=CO;③AD=BC中任意选取两个作为条件,“四边形ABCD是平行四边形”为结论构造命题. 
(1)以①②作为条件构成的命题是真命题吗?若是,请证明;若不是,请举出反例;
(2)写出按题意构成的所有命题中的假命题,并举出反例加以说明.(命题请写成“如果…,那么….”的形式)
参考答案:
【答案】
(1)解:以①②作为条件构成的命题是真命题,
证明:∵AB∥CD,
∴∠OAB=∠OCD,
在△AOB和△COD中,
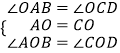 ,
,
∴△AOB≌△COD(ASA),
∴OB=OD,
∴四边形ABCD是平行四边形
(2)解:根据①③作为条件构成的命题是假命题,即如果有一组对边平行,另一组对边相等,那么四边形是平行四边形,如等腰梯形符合,但不是平行四边形; 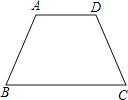
根据②③作为条件构成的命题是假命题,即如果一个四边形ABCD的对角线交于O,且OA=OC,AD=BC,那么这个四边形是平行四边形,如图,
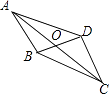
根据已知不能推出OB=OD或AD∥BC或AB=DC,即四边形不是平行四边形.
【解析】(1)根据平行得出全等三角形,即可求出OB=OD,根据平行四边形的判定推出即可;(2)根据等腰梯形和平行四边形的判定判断即可.
【考点精析】本题主要考查了平行四边形的判定和命题与定理的相关知识点,需要掌握两组对边分别平行的四边形是平行四边形:两组对边分别相等的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形;两组对角分别相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形;我们把题设、结论正好相反的两个命题叫做互逆命题.如果把其中一个叫做原命题,那么另一个叫做它的逆命题;经过证明被确认正确的命题叫做定理才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,AB=10,sin∠A=
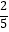 ,求BC的长和tan∠B的值.
,求BC的长和tan∠B的值. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明与甲、乙两人一起玩“手心手背”的游戏.他们约定:如果三人中仅有一人出“手心”或“手背”,则这个人获胜;如果三人都出“手心”或“手背”,则不分胜负,那么在一个回合中,如果小明出“手心”,则他获胜的概率是多少?(请用“画树状图”或“列表”等方法写出分析过程)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了解“课程选修”的情况,对报名参加“艺术鉴赏”,“科技制作”,“数学思维”,“阅读写作”这四个选修项目的学生(每人限报一课)进行抽样调查,下面是根据收集的数据绘制的不完整的统计图:

请根据图中提供的信息,解答下面的问题:
(1)此次共调查了名学生,扇形统计图中“艺术鉴赏”部分的圆心角是度;
(2)请把这个条形统计图补充完整;
(3)现该校共有800名学生报名参加这四个选修项目,请你估计其中有多少名学生选修“科技制作”项目. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知甲、乙两种原料中均含有A元素,其含量及每吨原料的购买单价如下表所示:
A元素含量
单价(万元/吨)
甲原料
5%
2.5
乙原料
8%
6
已知用甲原料提取每千克A元素要排放废气1吨,用乙原料提取每千克A元素要排放废气0.5吨,若某厂要提取A元素20千克,并要求废气排放不超过16吨,问:该厂购买这两种原料的费用最少是多少万元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线x=﹣4与x轴交于点E,一开口向上的抛物线过原点交线段OE于点A,交直线x=﹣4于点B,过B且平行于x轴的直线与抛物线交于点C,直线OC交直线AB于D,且AD:BD=1:3.

(1)求点A的坐标;
(2)若△OBC是等腰三角形,求此抛物线的函数关系式. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,菱形ABCD中,∠A=60°,点P从A出发,以2cm/s的速度沿边AB、BC、CD匀速运动到D终止,点Q从A与P同时出发,沿边AD匀速运动到D终止,设点P运动的时间为t(s).△APQ的面积S(cm2)与t(s)之间函数关系的图象由图2中的曲线段OE与线段EF、FG给出.
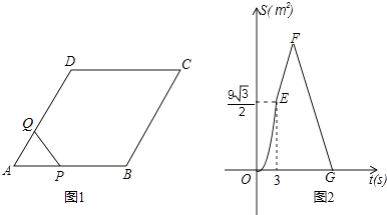
(1)求点Q运动的速度;
(2)求图2中线段FG的函数关系式;
(3)问:是否存在这样的t,使PQ将菱形ABCD的面积恰好分成1:5的两部分?若存在,求出这样的t的值;若不存在,请说明理由.
相关试题

