【题目】阅读理解题:在路上,我们经常看到这样的汽车牌照号:“辽A30803”,“辽P12321”,“京C76H67”,…,给人以对称美的感受.除了表示地区标志的汉字和字母(如:沈阳车牌辽A,葫芦岛车牌辽P等)以外,像“30803”、“76H67”这样的由数或由数和字母共同组成的车牌号,我们称之为“轴对称车牌号”.在正整数中,现定义为,“形如![]() 的正整数叫做轴对称数.”比如:99,363,2112等都是轴对称数.
的正整数叫做轴对称数.”比如:99,363,2112等都是轴对称数.
(1)写出最小的五位“轴对称数”;
(2)请你设计一个我们葫芦岛市的车牌号,要求:此车牌号的后五位是“轴对称车牌号”,且由数字和字母组成的;
(3)已知某车的车牌号是由数字组成的“轴对称车牌号”,设首位数字为m,去掉首尾数字后的中间的三位数为n.已知多项式x2﹣2m能用公式法分解因式,![]() n是多项式a﹣1与多项式a+102相乘得到的多项式的一次项系数,求出符合条件的车牌号.
n是多项式a﹣1与多项式a+102相乘得到的多项式的一次项系数,求出符合条件的车牌号.
参考答案:
【答案】(1)10001;(2)“辽P12O21”;(3)车牌号是27072或87078
【解析】
(1)根据轴对称数的定义写出最小的五位“轴对称数”;
(2)根据轴对称数的定义写出即可,但前面要加辽P;
(3)先根据多项式乘多项式的法则计算,再根据![]() n是多项式a-1与多项式a+102相乘得到的多项式的一次项系数,可得方程
n是多项式a-1与多项式a+102相乘得到的多项式的一次项系数,可得方程![]() n=101,求得n=707,再根据多项式x2-2m能用公式法分解因式,可得2m一定是完全平方数,可得m=2或m=8,从而得到符合条件的车牌号.
n=101,求得n=707,再根据多项式x2-2m能用公式法分解因式,可得2m一定是完全平方数,可得m=2或m=8,从而得到符合条件的车牌号.
解:(1)最小的五位“轴对称数”是10001;
(2)“辽P12O21”;
(3)∵(a﹣1)(a+102)=a2+102a﹣a﹣102=a2+101a﹣102,
∴![]() ,
,
∴n=707,
∵多项式x2﹣2m能用公式法分解因式,
∴2m一定是完全平方数,
又依题意可知,m是数字,且m≠0,
∴m=2或m=8.
因此这个车牌号是27072或87078.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场为吸引顾客,设立了一个可以自由转动的转盘,并规定每购买
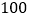 元商品可以获得一次转动转盘的机会,如果转盘停止转动时,指针正好落在红、绿、黄区域,那么顾客可以分别获得
元商品可以获得一次转动转盘的机会,如果转盘停止转动时,指针正好落在红、绿、黄区域,那么顾客可以分别获得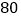 元、
元、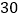 元、
元、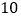 元购物券,如果不愿转动转盘,那么可以直接获得
元购物券,如果不愿转动转盘,那么可以直接获得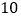 元购物券,设转盘停止转动时,指针正好落在红、绿、黄区域的概率依次为
元购物券,设转盘停止转动时,指针正好落在红、绿、黄区域的概率依次为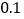 ,
,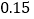 ,
,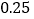 .
.(1)平均来说,每转动转盘
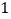 次所获得购物券的金额是多少?
次所获得购物券的金额是多少?(2)小明在家也做了一个同样的试验,转动转盘
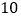 次后共得购物前
次后共得购物前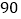 元,据此,小明认为,还是直接领取
元,据此,小明认为,还是直接领取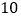 元购物券合算,你同意他的说法吗?
元购物券合算,你同意他的说法吗? -
科目: 来源: 题型:
查看答案和解析>>【题目】小敏的爸爸买了某项体育比赛的一张门票,她和哥哥两人都想去观看,可门票只有一张,读九年级哥哥想了一个办法,拿出
 张扑克牌,将数字
张扑克牌,将数字 、
、 、
、 、
、 的四张给了小敏,将数字
的四张给了小敏,将数字 、
、 、
、 、
、 的四张扑克牌留给自己,并按如下游戏规则进行:小敏和哥哥从各自的四张牌中随机抽出一张,然后将抽出两张牌数字相加,如果和为偶数,则小敏去;如果和为奇数,则哥哥去.
的四张扑克牌留给自己,并按如下游戏规则进行:小敏和哥哥从各自的四张牌中随机抽出一张,然后将抽出两张牌数字相加,如果和为偶数,则小敏去;如果和为奇数,则哥哥去.(1)请用画树形图或列表的方法求小敏去看比赛的概率;
(2)小敏知道哥哥设计的游戏规则不公平,于是她提议两人交换一张牌,使游戏规则公平后再进行比赛,你知道小敏是如何提议的吗?说说你的理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图显示了用计算机模拟随机投掷一枚图钉的某次实验的结果.

下面有三个推断:
①当投掷次数是500时,计算机记录“钉尖向上”的次数是308,所以“钉尖向上”的概率是0.616;
②随着实验次数的增加,“钉尖向上”的频率总在0.618附近摆动,显示出一定的稳定性,可以估计“钉尖向上”的概率是0.618;
③若再次用计算机模拟实验,则当投掷次数为1000时,“钉尖向上”的概率一定是0.620.
其中合理的是( )
A. ① B. ② C. ①② D. ①③
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰△ABC中,AB=BC,以BC为直径的⊙O与AC相交于点D,过点D作DE⊥AB交CB延长线于点E,垂足为点F.
(1)判断DE与⊙O的位置关系,并说明理由;
(2)若⊙O的半径R=5,tanC=
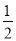 ,求EF的长.
,求EF的长.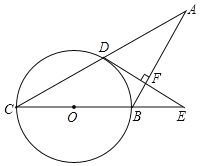
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△CAD与△CEB都是等边三角形,BD、EA的延长线相交于点F.
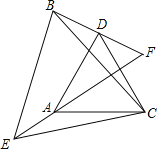
(1)求证:△ACE≌△DCB.
(2)求∠F的度数.
(3)若AD⊥BD,请直接写出线段EF与线段BD、DF之间的数量关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=﹣
 x+c与x轴交于点A(3,0),与y轴交于点B,抛物线y=﹣
x+c与x轴交于点A(3,0),与y轴交于点B,抛物线y=﹣ x2+bx+c经过点A,B.
x2+bx+c经过点A,B.(1)求点B的坐标和抛物线的解析式;
(2)M(m,0)为x轴上一动点,过点M且垂直于x轴的直线与直线AB及抛物线分别交于点P,N.
①点M在线段OA上运动,若以B,P,N为顶点的三角形与△APM相似,求点M的坐标;
②点M在x轴上自由运动,若三个点M,P,N中恰有一点是其它两点所连线段的中点(三点重合除外),则称M,P,N三点为“共谐点”.请直接写出使得M,P,N三点成为“共谐点”的m的值.

相关试题

