【题目】如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD及等边△ABE,已知:∠BAC=30°,EF⊥AB,垂足为F,连接DF. 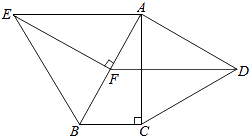
(1)试说明AC=EF;
(2)求证:四边形ADFE是平行四边形.
参考答案:
【答案】
(1)证明:∵Rt△ABC中,∠BAC=30°,
∴AB=2BC,
又∵△ABE是等边三角形,EF⊥AB,
∴AB=2AF
∴AF=BC,
在Rt△AFE和Rt△BCA中,
![]() ,
,
∴Rt△AFE≌Rt△BCA(HL),
∴AC=EF;
(2)∵△ACD是等边三角形,
∴∠DAC=60°,AC=AD,
∴∠DAB=∠DAC+∠BAC=90°
又∵EF⊥AB,
∴EF∥AD,
∵AC=EF,AC=AD,
∴EF=AD,
∴四边形ADFE是平行四边形.
【解析】(1)首先由Rt△ABC中,由∠BAC=30°可以得到AB=2BC,又由△ABE是等边三角形,EF⊥AB,由此得到AE=2AF,并且AB=2AF,然后证得△AFE≌△BCA,继而证得结论;(2)根据(1)知道EF=AC,而△ACD是等边三角形,所以EF=AC=AD,并且AD⊥AB,而EF⊥AB,由此得到EF∥AD,再根据平行四边形的判定定理即可证明四边形ADFE是平行四边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据问题进行计算:
(1)计算: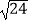 ×
× 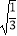 ﹣4×
﹣4× 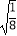 ×(1﹣
×(1﹣ 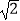 )0;
)0;
(2)已知三角形两边长为3,5,要使这个三角形是直角三角形,求出第三边的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:x 2 -(x+2)(2-x)-2(x-5)2 ,其中x=3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某港口位于东西方向的海岸线上.“远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里.它们离开港口
 小时后相距30海里.如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗?
小时后相距30海里.如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗? 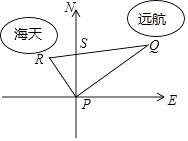
-
科目: 来源: 题型:
查看答案和解析>>【题目】)计算:
(1)﹣5×(﹣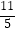 )+13×(﹣
)+13×(﹣ 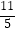 )﹣3÷(﹣
)﹣3÷(﹣ 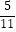 )
)
(2)﹣12012×[(﹣2)5﹣32﹣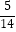 ÷(﹣
÷(﹣  )]﹣2.
)]﹣2. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,AC是对角线,今有较大的直角三角板,一边始终经过点B,直角顶点P在射线AC上移动,另一边交DC于Q.
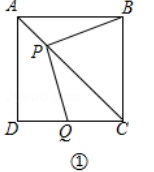
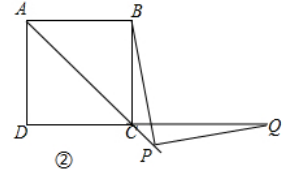
(1)如图①,当点Q在DC边上时,猜想并写出PB与PQ所满足的数量关系,并加以证明;
(2)如图②,当点Q落在DC的延长线上时,猜想并写出PB与PQ满足的数量关系,并证明你的猜想. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算1052-952的结果为( )
A. 1000 B. 1980
C. 2000 D. 4000
相关试题

