【题目】某港口位于东西方向的海岸线上.“远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里.它们离开港口 ![]() 小时后相距30海里.如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗?
小时后相距30海里.如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗? 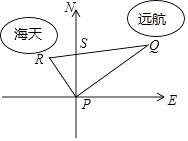
参考答案:
【答案】解:根据题意,得 PQ=16×1.5=24(海里),
PR=12×1.5=18(海里),
QR=30(海里),
∵242+182=302 ,
即PQ2+PR2=QR2 ,
∴∠QPR=90°.
由“远洋号”沿东北方向航行可知,∠QPS=45°,则∠SPR=45°,
即“海天”号沿西北方向航行.
【解析】根据路程=速度×时间分别求得PQ、PR的长,再进一步根据勾股定理的逆定理可以证明三角形PQR是直角三角形,从而求解.
【考点精析】通过灵活运用勾股定理的逆定理,掌握如果三角形的三边长a、b、c有下面关系:a2+b2=c2,那么这个三角形是直角三角形即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)解方程4x2-(x+1)2=0;
(2)请运用解一元二次方程的思想方法解方程x3-x=0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据问题进行计算:
(1)计算: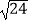 ×
× 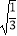 ﹣4×
﹣4× 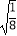 ×(1﹣
×(1﹣ 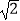 )0;
)0;
(2)已知三角形两边长为3,5,要使这个三角形是直角三角形,求出第三边的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:x 2 -(x+2)(2-x)-2(x-5)2 ,其中x=3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD及等边△ABE,已知:∠BAC=30°,EF⊥AB,垂足为F,连接DF.
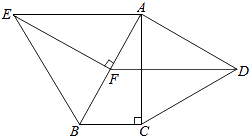
(1)试说明AC=EF;
(2)求证:四边形ADFE是平行四边形. -
科目: 来源: 题型:
查看答案和解析>>【题目】)计算:
(1)﹣5×(﹣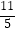 )+13×(﹣
)+13×(﹣ 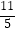 )﹣3÷(﹣
)﹣3÷(﹣ 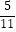 )
)
(2)﹣12012×[(﹣2)5﹣32﹣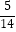 ÷(﹣
÷(﹣  )]﹣2.
)]﹣2. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,AC是对角线,今有较大的直角三角板,一边始终经过点B,直角顶点P在射线AC上移动,另一边交DC于Q.
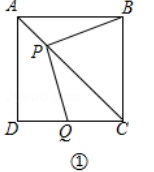
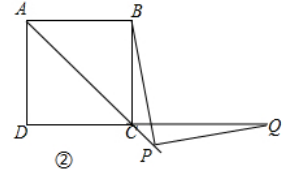
(1)如图①,当点Q在DC边上时,猜想并写出PB与PQ所满足的数量关系,并加以证明;
(2)如图②,当点Q落在DC的延长线上时,猜想并写出PB与PQ满足的数量关系,并证明你的猜想.
相关试题

