【题目】如图,点![]() ,过点
,过点![]() 做直线
做直线![]() 平行于
平行于![]() 轴,点
轴,点![]() 关于直线
关于直线![]() 对称点为
对称点为![]() .
.

(1)求点![]() 的坐标;
的坐标;
(2)点![]() 在直线
在直线![]() 上,且位于
上,且位于![]() 轴的上方,将
轴的上方,将![]() 沿直线
沿直线![]() 翻折得到
翻折得到![]() ,若点
,若点![]() 恰好落在直线
恰好落在直线![]() 上,求点
上,求点![]() 的坐标和直线
的坐标和直线![]() 的解析式;
的解析式;
(3)设点![]() 在直线
在直线![]() 上,点
上,点![]() 在直线
在直线![]() 上,当
上,当![]() 为等边三角形时,求点
为等边三角形时,求点![]() 的坐标.
的坐标.
参考答案:
【答案】(1)(3,0);(2)A(1,![]() );直线BD为
);直线BD为![]() ;(3)点P的坐标为(
;(3)点P的坐标为(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
【解析】
(1)根据题意,点B、C关于点M对称,即可求出点C的坐标;
(2)由折叠的性质,得AB=CB,BD=AD,根据勾股定理先求出AM的长度,设点D为(1,a),利用勾股定理构造方程,即可求出点D坐标,然后利用待定系数法求直线BD.
(3)分两种情形:如图2中,当点P在第一象限时,连接BQ,PA.证明点P在AC的垂直平分线上,构建方程组求出交点坐标即可.如图3中,当点P在第三象限时,同法可得△CAQ≌△CBP,可得∠CAQ=∠CBP=30°,构建方程组解决问题即可.
解:(1)根据题意,
∵点B、C关于点M对称,且点B、M、C都在x轴上,
又点B(![]() ),点M(1,0),
),点M(1,0),
∴点C为(3,0);
(2)如图:

由折叠的性质,得:AB=CB=4,AD=CD=BD,
∵BM=2,∠AMB=90°,
∴![]() ,
,
∴点A的坐标为:(1,![]() );
);
设点D为(1,a),则DM=a,BD=AD=![]() ,
,
在Rt△BDM中,由勾股定理,得
![]() ,
,
解得:![]() ,
,
∴点D的坐标为:(1,![]() );
);
设直线BD为![]() ,则
,则
 ,解得:
,解得: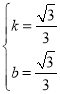 ,
,
∴直线BD为:![]() ;
;
(3)如图2中,当点P在第一象限时,连接BQ,PA.
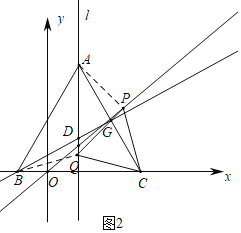
∵△ABC,△CPQ都是等边三角形,
∴∠ACB=∠PCQ=60°,
∴∠ACP=∠BCQ,
∵CA=CB,CP=CQ,
∴△ACP≌△BCQ(SAS),
∴AP=BQ,
∵AD垂直平分线段BC,
∴QC=QB,
∴PA=PC,
∴点P在AC的垂直平分线上,
由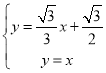 ,解得
,解得 ,
,
∴P(![]() ,
,![]() ).
).
如图3中,当点P在第三象限时,同法可得△CAQ≌△CBP,
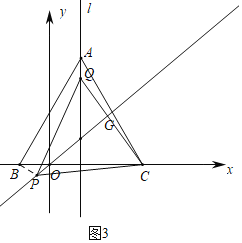
∴∠CAQ=∠CBP=30°,
∵B(-1,0),
∴直线PB的解析式为![]() ,
,
由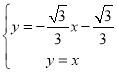 ,解得:
,解得: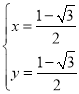 ,
,
∴P(![]() ,
,![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将等边
 沿
沿 翻折得
翻折得 ,
, ,点
,点 为直线
为直线 上的一个动点,连接
上的一个动点,连接 ,将线段
,将线段 绕点
绕点 顺时针旋转
顺时针旋转 的角度后得到对应的线段
的角度后得到对应的线段 (即
(即 ),
), 交
交 于点
于点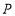 ,则下列结论:①
,则下列结论:① ;②
;② ;③当
;③当 为线段
为线段 的中点时,则
的中点时,则 ;④四边形
;④四边形 的面积为
的面积为 ;⑤连接
;⑤连接 、
、 ,当
,当 的长度最小时,则
的长度最小时,则 的面积为
的面积为 .则说法正确的有________(只填写序号)
.则说法正确的有________(只填写序号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】2019年是中国建国70周年,作为新时期的青少年,我们应该肩负起实现祖国伟大复兴的责任,为了培养学生的爱国主义情怀,我校学生和老师在5月下旬集体乘车去抗日战争纪念馆研学,已知学生的人数是老师人数的12倍多20人,学生和老师总人数有540人.
(1)请求出去抗日战争纪念馆研学的学生和老师的人数各是多少?
(2)如果学校准备租赁
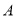 型车和
型车和 型车共14辆(其中
型车共14辆(其中 型车最多7辆),已知
型车最多7辆),已知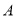 型车每年最车可以载35人,
型车每年最车可以载35人, 型车每车最多可以载45人,共有几种租车方案?
型车每车最多可以载45人,共有几种租车方案?(3)已知
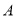 型车日租金为2000元,
型车日租金为2000元, 型车日租金为3000元,设租赁
型车日租金为3000元,设租赁 型大巴车
型大巴车 辆,求出租赁总租金为
辆,求出租赁总租金为 元与
元与 的函数解析式,并求出最经济的租车方案.
的函数解析式,并求出最经济的租车方案. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知
 ,
, ,且
,且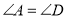 ,
,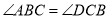 .
.
(1)求证:
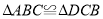 ;
;(2)如图2,若
 ,
, ,折叠纸片,使点
,折叠纸片,使点 与点
与点 重合,折痕为
重合,折痕为 ,且
,且 .
.①求证:
 ;
;②点
 是线段
是线段 上一点,连接
上一点,连接 ,一动点
,一动点 从点
从点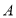 出发,沿线段
出发,沿线段 以每秒1个单位的速度运动到点
以每秒1个单位的速度运动到点 ,再沿线段
,再沿线段 以每秒
以每秒 个单位的速度运动到
个单位的速度运动到 后停止,点
后停止,点 在整个运动过程中用时最少多少秒?
在整个运动过程中用时最少多少秒? -
科目: 来源: 题型:
查看答案和解析>>【题目】某校八年级全体同学参加了爱心捐款活动,该校随机抽查了部分同学捐款的情况统计如图:
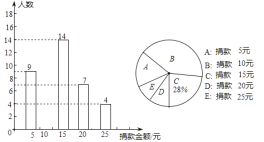
(1)求出本次抽查的学生人数,并将条形统计图补充完整;
(2)捐款金额的众数是___________元,中位数是_____________;
(3)请估计全校八年级1000名学生,捐款20元的有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(-3,2)、B(0,4)、C(0,2),
(1)画出△ABC关于点C成中心对称的△A1B1C;
(2)平移△ABC:若点A的对应点A2的坐标为(0,-4),画出平移后对应的△A2B2C2;
(3)△A1B1C和△A2B2C2关于某一点成中心对称,则对称中心的坐标为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数
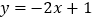 的图象与y轴交于点A,点B(-1,n)是该函数图象与反比例函数
的图象与y轴交于点A,点B(-1,n)是该函数图象与反比例函数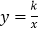 (k≠0)图象在第二象限内的交点.
(k≠0)图象在第二象限内的交点.(1)求点B的坐标及k的值;
(2)试在x轴上确定点C,使AC=AB,请直接写出点C的坐标.
相关试题

