【题目】 如图,数轴上点A对应的有理数为10,点P以每秒1个单位长度的速度从点A出发,点Q以每秒3个单位长度的速度从原点O出发,且P、Q两点同时向数轴正方向运动,设运动时间为t秒.
(1)当t=2时,P,Q两点对应的有理数分別是 , ,PQ= ;
(2)当PQ=8时,求t的值.
![]()
参考答案:
【答案】(1)12;6;6;(2)t的值为1秒或9秒.
【解析】
(1)结合数轴,根据P、Q运动的速度和时间计算出即可;
(2)当PQ=8时,分两种情况:当点P在点Q左侧时,当点P在点Q左侧时.
解:(1)∵10+2×1=12,3×2=6,
∴当t=2时,P,Q两点对应的有理数分别是12,6,
∴PQ=12﹣6=6.
故答案为:12;6;6;
(2)运动t秒时,P,Q两点对应的有理数分别是10+t,3t.
①当点P在点Q右侧时,
∵PQ=8,
∴(10+t)﹣3t=8,
解得:t=1;
②当点P在点Q左侧时,
∵PQ=8,
∴3t﹣(10+t)=8,
解得:t=9.
综上所述,t的值为1秒或9秒.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:在数轴上A点表示数0,B点表示的数是最小的正整数,C点表示数5,点A与点B之间的距离表示为AB,点A与点C之间的距离表示为AC,点B与点C之间的距离表示为BC.

(1) BC= .
(2) A,B,C在数轴上同时运动,点B和点C分别以每秒3个单位长度和6个单位长度的速度向右运动,点A以每秒a个单位长度的速度向左运动。在运动过程中,3BC-2AB的值始终保持不变,请求出a的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,某超市从一楼到二楼有一自动扶梯,图②是侧面示意图.已知自动扶梯AB的坡度为1∶2.4,AB的长度是13米,MN是二楼楼顶,MN∥PQ , C是MN上处在自动扶梯顶端B点正上方的一点,BC⊥MN , 在自动扶梯底端A处测得C点的仰角为42°,则二楼的层高BC约为(精确到0.1米,sin42°≈0.67,tan42°≈0.90)( )

A.10.8米
B.8.9米
C.8.0米
D.5.8米 -
科目: 来源: 题型:
查看答案和解析>>【题目】直角△ABC中,斜边AB=5,直角边BC、AC之长是一元二次方程x2﹣(2m﹣1)x+4(m﹣1)=0的两根,则m的值为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1) ﹣3
﹣3  ×(
×(  ﹣
﹣  )
)
(2) ﹣
﹣ 

(3)sin230°+2sin60°+tan45°﹣tan60°+cos230°. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知线段AB=12cm,点C是直线AB上任意一点,M、N分别是AC、BC的中点,则线段MN=________cm.
-
科目: 来源: 题型:
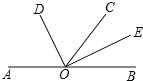
查看答案和解析>>【题目】如图,点A,O,B在同一直线上,射线OD和射线OE分别平分∠AOC和∠BOC.
(1)当∠BOE=25°时,求∠AOD的度数
(2)在图中找出∠COD的补角,并说明理由.
相关试题

