【题目】在四边形ABCD中,AD∥BC,DE平分∠ADB,∠BDC=∠C.若∠ABD的平分线与CD的延长线交于F,且∠F=x°(其中0<x<90),则∠ABC=°,(用含有x的式子表示) 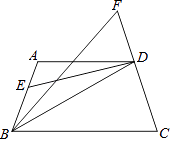
参考答案:
【答案】(180﹣2x)
【解析】解:如图, 
∵AD∥BC,
∴∠ADF=∠C=∠BDC,
∵∠EDA=∠EDB,
∴∠ADF+∠EDA=90°,即∠EDF=90°
∴∠3=90°﹣x,
∵∠3=∠1+∠2= ![]() (∠ABD+∠ADB)=
(∠ABD+∠ADB)= ![]() (180°﹣∠A)=90°﹣
(180°﹣∠A)=90°﹣ ![]() ∠A,
∠A,
∴90°﹣x=90°﹣ ![]() ∠A,
∠A,
∴∠A=2x,
∵∠A+∠ABC=180°,
∴∠ABC=180°﹣2x.
所以答案是180﹣2x.
【考点精析】关于本题考查的平行线的性质和多边形内角与外角,需要了解两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补;多边形的内角和定理:n边形的内角和等于(n-2)180°.多边形的外角和定理:任意多边形的外角和等于360°才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学九年级数学兴趣小组想测量建筑物AB的高度.他们在C处仰望建筑物顶端,测得仰角为48°,再往建筑物的方向前进6米到达D处,测得仰角为64°,求建筑物的高度.(测角器的高度忽略不计,结果精确到0.1米)
(参考数据:sin48°≈
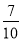 ,tan48°≈
,tan48°≈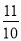 ,sin64°≈
,sin64°≈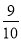 ,tan64°≈2)
,tan64°≈2)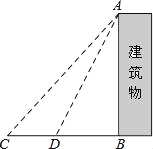
-
科目: 来源: 题型:
查看答案和解析>>【题目】化简:
(1)a﹣b﹣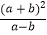 ;
;
(2)(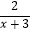 +
+ 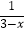 )÷
)÷ 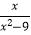 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:x3﹣49x=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在△ABC中任意一点P(x0 , y0),经平移后对应点为P1(x0+3,y0﹣3),将△ABC作同样平移得到△DEF.
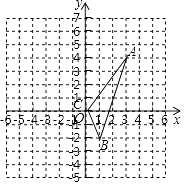
(1)求△ABC的面积;
(2)请写出D,E,F的坐标,并在图中画出△DEF. -
科目: 来源: 题型:
查看答案和解析>>【题目】去括号,并合并同类项:3x+1﹣2(4﹣x)= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】制造一种产品,原来每件成本是100元,由于连续两次降低成本,现在的成本是81元,则平均每次降低的百分率是( )
A.8.5%
B.9%
C.9.5%
D.10%
相关试题

