【题目】如图所示,某地有一座圆弧形的拱桥,桥下水面宽AB为12米,拱高CD为4米.
(1)求这座拱桥所在圆的半径.
(2)现有一艘宽5米,船舱顶部为正方形并高出水面3.6米的货船要经过这里,此时货船能顺利通过这座拱桥吗?请说明理由.

参考答案:
【答案】(1)这座拱桥所在圆的半径为6.5米;(2)货船不能顺利通过这座拱桥.
【解析】
(1)首先连接OA,设这座拱桥所在圆的半径为x米,由垂径定理,易得方程:x2=(x-4)2+62,解此方程即可求得答案;
(2)连接OM,设MN = 5米,可求得此时OH的高,即可求得OH-OD的长,比较3.6米,即可得到此时货船能否顺利通过这座拱桥.
(1)连结OA,
根据题意,得CD=4米,AB=12米,则AD=![]() AB=6(米).
AB=6(米).
设这座拱桥所在圆的半径为x米,
则OA=OC=x米,OD=OC-CD=(x-4)米.
在Rt△AOD中,OA2=OD2+AD2,
即x2=(x-4)2+62,
解得x=6.5,
故这座拱桥所在圆的半径为6.5米.
(2)货船不能顺利通过这座拱桥.理由:
连结OM,设MN=5米,
∵OC⊥MN,∴MH=![]() MN=2.5(米).
MN=2.5(米).
在Rt△OMH中,OH=![]() =6(米).
=6(米).
∵OD=OC-CD=6.5-4=2.5(米),
∴OH-OD=6-2.5=3.5(米)<3.6米,
∴货船不能顺利通过这座拱桥.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB="AC," AB+BC=8.将△ABC折叠,使得点A落在点B处,折痕DF分别与AB、AC交于点D、F,连接BF,则△BCF的周长是( )
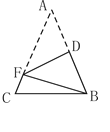
A.8B.16C.4D.10
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O是△ABC的外接圆,AC为直径,弦BD=BA,BE⊥DC交DC的延长线于点E,求证:

(1)∠1=∠BAD;
(2)BE是⊙O的切线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,AB⊥BC,DC⊥BC,B、C分别是垂足,DE交AC于M,BC=CD,AB=EC,DE与AC有什么关系?请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC内接于⊙O,AB=AC,CO的延长线交AB于点D.
(1)求证:AO平分∠BAC;
(2)若BC=6,sin∠BAC=
 ,求AC和CD的长.
,求AC和CD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是交警在一个路口统计的某个时段往车辆的车速情况(单位:千米/时).则这些车辆行驶速度的中位数是________、众数是________、平均数是________(结果精确到
 ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市市民在创建文明城市的活动中,通过向市文明办发送短信,积极献言建策.去年
 月
月 今年
今年 月期间,每月发送的短信条数依次为:
月期间,每月发送的短信条数依次为: 、
、 、
、 、
、 、
、 .在这组数据中,众数和中位数分别是________.
.在这组数据中,众数和中位数分别是________.
相关试题

