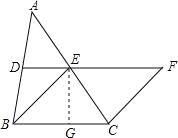
【题目】如图,在△ABC中,DE分别是AB,AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连CF
(1)求证:四边形BCFE是菱形;
(2)若CE=6,∠BEF=120°,求菱形BCFE的面积.

参考答案:
【答案】(1)证明见解析(2)18![]()
【解析】从所给的条件可知,DE是△ABC中位线,所以DE∥BC且2DE=BC,所以BC和EF平行且相等,所以四边形BCFE是平行四边形,又因为BE=FE,所以是菱形;∠BCF是120°,所以∠EBC为60°,所以菱形的边长也为6,求出菱形的高面积就可求.
解:(1)证明:∵D、E分别是AB、AC的中点,
∴DE∥BC且2DE=BC,
又∵BE=2DE,EF=BE,
∴EF=BC,EF∥BC,
∴四边形BCFE是平行四边形,
又∵BE=EF,
∴四边形BCFE是菱形;
(2)解:∵∠BEF=120°,
∴∠EBC=60°,
∴△EBC是等边三角形,
∴BE=BC=CE=6,
过点E作EG⊥BC于点G,
∴EG=BEsin60°=6×![]() =3
=3![]() ,
,
∴S菱形BCFE=BCEG=6×3![]() =18
=18![]() .
.
“点睛”本题考查菱形的判定和性质以及三角形中位线定理,以及菱形的面积的计算等知识点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的一元二次方程x2+2x+2m=0有两个不相等的实数根.
(1)求m的取值范围;
(2)若x1,x2是一元二次方程x2+2x+2m=0的两个根,且x12+x22=8,求m的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在宽为20m,长为32m的矩形地面上修筑同样宽的道路(图中阴影部分),余下的部分种上草坪.要使草坪的面积为540m2,求道路的宽.
(部分参考数据:322=1024,522=2704,482=2304)

-
科目: 来源: 题型:
查看答案和解析>>【题目】(a-3)(a-5)+1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一种面粉的质量标识为“26±0.25千克”,则下列面粉中合格的是:( )
A.26.30千克
B.25.70千克
C.26.51千克
D.25.80千克 -
科目: 来源: 题型:
查看答案和解析>>【题目】(ab+1)2-(ab-1)2
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值: (2x-3y)2-(2x+y)(2x-y), 其中x=-1, y=-2
相关试题

