【题目】综合:
(1)如图1,纸片ABCD中,AD=5,SABCD=15,过点A作AE⊥BC,垂足为E,沿AE剪下△ABE,将它平移至△DCE'的位置,拼成四边形AEE'D,则四边形AEE'D的形状为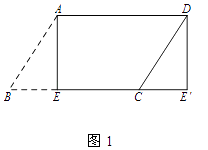
A.平行四边形
B.菱形
C.矩形
D.正方形
(2)如图2,在(1)中的四边形纸片AEE'D中,在EE'上取一点F,使EF=4,剪下△AEF,剪下△AEF,将它平移至△DE'F'的位置,拼成四边形AFF'D.
①求证:四边形AFF'D是菱形;
②求四边形AFF'D的两条对角线的长.
参考答案:
【答案】
(1)C
(2)解:如图2中,
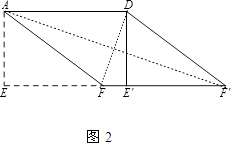
①证明:∵AD=5,S□ABCD=15,
∴AE=3.
又∵在图2中,EF=4,
∴在Rt△AEF中,AF═5.
∴AF=AD=5,
又∵AF∥DF',AF=DF,
∴四边形AFF'D是平行四边形.
∴四边形AFF'D是菱形.
②解:连接AF',DF,
在Rt△DE'F中,∵E'F=E'E﹣EF=5﹣4=1,DE'=3,
∴DF═ ![]() =
= ![]() .
.
在Rt△AEF'中,∵EF'=E'E+E'F'=5+4=9,AE=3,
∴AF'═ ![]() =
= ![]() =3
=3 ![]()
【解析】(1)解:如图1中,
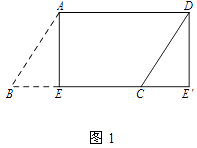
∵四边形ABCD是平行四边形,
∴AD=BC,
∵BE=CE′,
∴AD∥EE′,AD=EE′,
∴四边形AEE′D是平行四边形,
∵∠AEE′=90°,
∴四边形AEE′D是矩形,
故选C.
【考点精析】本题主要考查了矩形的判定方法的相关知识点,需要掌握有一个角是直角的平行四边形叫做矩形;有三个角是直角的四边形是矩形;两条对角线相等的平行四边形是矩形才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F.若BF=12,AB=10,则AE的长为( )

A.10
B.12
C.16
D.18 -
科目: 来源: 题型:
查看答案和解析>>【题目】两条平行线间的距离公式 一般地;两条平行线l1:Ax+By+C1=0和l2:Ax+By+C2=0间的距离公式是d=
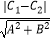 如:求:两条平行线x+3y﹣4=0和2x+6y﹣9=0的距离.
如:求:两条平行线x+3y﹣4=0和2x+6y﹣9=0的距离.
解:将两方程中x,y的系数化成对应相等的形式,得2x+6y﹣8=0和2x+6y﹣9=0,因此,d= 两条平行线l1:3x+4y=10和l2:6x+8y﹣10=0的距离是 .
两条平行线l1:3x+4y=10和l2:6x+8y﹣10=0的距离是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A. a3a2=a6B. a8÷a2=a4C. (a3)2=a6D. a+2a2=3a2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,直线y=﹣2x+a与y轴交于点C (0,6),与x轴交于点B.
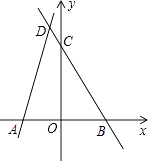
(1)求这条直线的解析式;
(2)直线AD与(1)中所求的直线相交于点D(﹣1,n),点A的坐标为(﹣3,0). ①求n的值及直线AD的解析式;
②求△ABD的面积;
③点M是直线y=﹣2x+a上的一点(不与点B重合),且点M的横坐标为m,求△ABM的面积S与m之间的关系式. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(﹣4)2015(0.25)2014= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC中,∠C=90°,AD平分∠BAC交BC于点D,且CD=4cm,则点D到AB的距离是________.
相关试题

