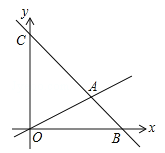
【题目】如图,在平面直角坐标系中,直线![]() 与x和y轴分别交于点B和点C,与直线OA相交于点A(4,2),动点M在线段OA和射线AC上运动.
与x和y轴分别交于点B和点C,与直线OA相交于点A(4,2),动点M在线段OA和射线AC上运动.
(1)求点B和点C的坐标.
(2)求△OAC的面积.
(3)是否存在点M,使△OMC的面积是△OAC的面积的![]() ?若存在,求出此时点M的坐标,若不存在,说明理由.
?若存在,求出此时点M的坐标,若不存在,说明理由.
参考答案:
【答案】(1)点B的坐标为(6,0),点C的坐标为(0,6);(2)12;(3)M的坐标是:M(1, ![]() )或M(1,5)或(﹣1,7)
)或M(1,5)或(﹣1,7)
【解析】试题分析:(1)在y=-x+6中, 分别令x=0,y=0即可得到结论;
(2)根据三角形面积公式计算即可;
(3)根据三角形的面积公式可判断M的横坐标是1,然后把x=1分别代入OA和AC的解析式中计算对应的函数值即可得到M点的坐标.
试题解析:解:(1)设y = 0,则x = 6;设x = 0,则y = 6,故点B的坐标为(6,0),点C的坐标为(0,6);
(2)S△OAC = ![]() OC×xA=
OC×xA=![]() ×6×4 =12;
×6×4 =12;
(3)存在点M使S△OMC=![]() S△OAC.
S△OAC.
设M的坐标为(x,y);OA的解析式是y=mx,则4m =2,
解得:m=![]() ,则直线OA的解析式是:y=
,则直线OA的解析式是:y=![]() x.
x.
∵当S△OMC= ![]() S△OAC时,即
S△OAC时,即![]() ×OC×|x|=
×OC×|x|=![]() ×12.
×12.
又∵OC=6,∴x =±1.
①当M在线段OA上时,x>0,所以x=1时,y=![]() ,则M的坐标是(1,
,则M的坐标是(1, ![]() );
);
②当M在射线AC:y=﹣x+6上时,由x=1,得y=5,则M的坐标是(1,5);由x=-1,得y=7,则M的坐标是(-1,7).

综上所述:M的坐标是:M(1, ![]() )或M(1,5)或(﹣1,7).
)或M(1,5)或(﹣1,7).
-
科目: 来源: 题型:
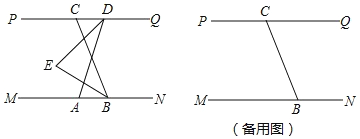
查看答案和解析>>【题目】如图,已知 MN∥PQ,B 在 MN 上,C 在 PQ 上,A 在 B 的左侧,D 在 C 的右侧,DE 平分∠ADC,BE平分∠ABC,直线 DE,BE 交于点 E,∠CBN=120°.
(1)若∠ADQ=110°,求∠BED 的度数;
(2)将线段 AD 沿 DC 方向平移,使得点 D 在点 C 的左侧,其他条件不变,若∠ADQ=n°,求∠BED 的度数(用含 n 的代数式表示)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,所有正方形的中心均在坐标原点,且各边与x轴或y轴平行,从内到外,它们的边长依次为2,4,6,8 …,顶点依次为A1,A2,A3,A4,A5,…,则顶点A55的坐标是( )

A. (13,13) B. (-13,-13) C. (-14,-14) D. (14,14)
-
科目: 来源: 题型:
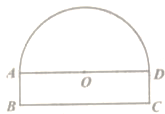
查看答案和解析>>【题目】如图,隧道的截面由半圆和长方形构成,长方形的长BC为8m,宽AB为1m,该隧道内设双向行驶的车道(共有2条车道),若现有一辆货运卡车高4m,宽2.3m。则这辆货运卡车能否通过该隧道?说明理由.
-
科目: 来源: 题型:
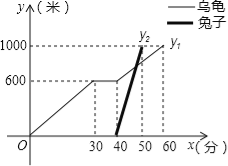
查看答案和解析>>【题目】“龟兔首次赛跑”之后,输了比赛的兔子没有气馁,总结反思后,和乌龟约定再赛一场.图中的函数图象刻画了“龟兔再次赛跑”的故事(x表示乌龟从起点出发所行的时间,y1表示乌龟所行的路程,y2表示兔子所行的路程).有下列说法:
①“龟兔再次赛跑”的路程为1000米;
②兔子和乌龟同时从起点出发;
③乌龟在途中休息了10分钟;
④兔子在途中750米处追上乌龟.
其中正确的说法是 .(把你认为正确说法的序号都填上)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某小区为了绿化环境,计划分两次购进A、B两种花草,第一次分别购进A、B两种花草30棵和15棵,共花费675元;第二次分别购进A、B两种花草12棵和5棵.两次共花费940元(两次购进的A、B两种花草价格均分别相同).
(1)A、B两种花草每棵的价格分别是多少元?
(2)若购买A、B两种花草共31棵,且B种花草的数量少于A种花草的数量的2倍,请你给出一种费用最省的方案,并求出该方案所需费用. -
科目: 来源: 题型:
查看答案和解析>>【题目】某水果专卖店销售樱桃,其进价为每千克
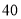 元,按每千克
元,按每千克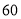 元出售,平均每天可售出
元出售,平均每天可售出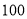 千克,后来经过市场调查发现,单价每千克降低
千克,后来经过市场调查发现,单价每千克降低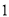 元,则平均每天的销售可增加
元,则平均每天的销售可增加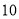 千克,若该专卖店销售这种樱桃要想平均每天获利
千克,若该专卖店销售这种樱桃要想平均每天获利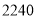 元,请回答:
元,请回答:(
 )每千克樱桃应降价多少元?
)每千克樱桃应降价多少元?(
 )在平均每天获利不变的情况下,为尽可能让利于顾客,赢得市场,该店应按原售价的几折出售?
)在平均每天获利不变的情况下,为尽可能让利于顾客,赢得市场,该店应按原售价的几折出售?
相关试题

