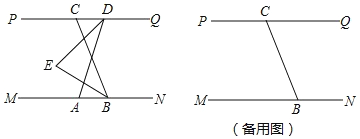
【题目】如图,已知 MN∥PQ,B 在 MN 上,C 在 PQ 上,A 在 B 的左侧,D 在 C 的右侧,DE 平分∠ADC,BE平分∠ABC,直线 DE,BE 交于点 E,∠CBN=120°.
(1)若∠ADQ=110°,求∠BED 的度数;
(2)将线段 AD 沿 DC 方向平移,使得点 D 在点 C 的左侧,其他条件不变,若∠ADQ=n°,求∠BED 的度数(用含 n 的代数式表示)
参考答案:
【答案】(1)65°;(2)∠BED=210°﹣(![]() n)°或(
n)°或(![]() n)°﹣30°或 30°﹣(
n)°﹣30°或 30°﹣(![]() n)°.
n)°.
【解析】(1)如图1中,延长DE交MN于H.利用∠BED=∠EHB+∠EBH,即可解决问题;
(2)分三种情形讨论即可解决问题.
(1)如图 1 中,延长 DE 交 MN 于 H.
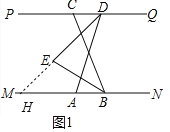
∵∠ADQ=110°,ED 平分∠ADP,
∴∠PDH=![]() ∠PDA=35°,
∠PDA=35°,
∵PQ∥MN,
∴∠EHB=∠PDH=35°,
∵∠CBN=120°,EB 平分∠ABC,
∴∠EBH=![]() ∠ABC=30°,
∠ABC=30°,
∴∠BED=∠EHB+∠EBH=65°.
(2)有 3 种情形,如图 2 中,当点 E 在直线 MN 与直线 PQ 之间时.延长 DE 交 MN 于 H.
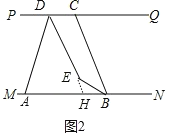
∵PQ∥MN,
∴∠QDH=∠DHA=![]() n°,
n°,
∴∠BED=∠EHB+∠EBH=180°﹣(![]() n)°+30°=210°﹣(
n)°+30°=210°﹣(![]() n)°,
n)°,
当点 E 在直线 MN 的下方时,如图 3 中,
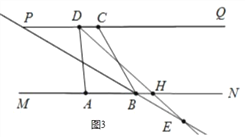
设 DE 交 MN 于 H.
∵∠PBC=∠ABP=30°,
∴∠HBE=∠ABP=30°(对顶角).
∵∠ADH=∠CDH=(![]() n)°,
n)°,
∴∠CDH=∠DHB=(![]() n)°(两直线平行,内错角相等).
n)°(两直线平行,内错角相等).
又∵∠DHB=∠HBE+∠HEB,
∴∠BED=(![]() n)°﹣30°,
n)°﹣30°,
当点 E 在 PQ 上方时,如图 4 中,
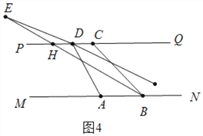
设 PQ 交 BE 于 H.同法可得∠BED=30°﹣(![]() n)°.
n)°.
综上所述,∠BED=210°﹣(![]() n)°或(
n)°或(![]() n)°﹣30°或 30°﹣(
n)°﹣30°或 30°﹣(![]() n)°.
n)°.
-
科目: 来源: 题型:
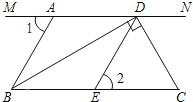
查看答案和解析>>【题目】如图,MN∥BC,BD⊥DC,∠1=∠2=60°.
(1)AB 与 DE 平行吗?请说明理由;
(2)若 DC 是∠NDE 的平分线.
①试说明∠ABC=∠C;
②试说明 BD 是∠ABC 的平分线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线l1∥l2,直线l3和直线l1、l2交于点C和D,在直线CD上有一点P.

(1)如果P点在C、D之间运动时,问∠PAC,∠APB,∠PBD有怎样的数量关系?请说明理由.
(2)若点P在C、D两点的外侧运动时(P点与点C、D不重合),试探索∠PAC,∠APB,∠PBD之间的关系又是如何?
-
科目: 来源: 题型:
查看答案和解析>>【题目】为解决江北学校学生上学过河难的问题,乡政府决定修建一座桥,建桥过程中需测量河的宽度(即两平行河岸AB与MN之间的距离).在测量时,选定河对岸MN上的点C处为桥的一端,在河岸点A处,测得∠CAB=30°,沿河岸AB前行30米后到达B处,在B处测得∠CBA=60°,请你根据以上测量数据求出河的宽度.(参考数据:
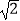 ≈1.41,
≈1.41, 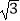 ≈1.73,结果保留整数)
≈1.73,结果保留整数) 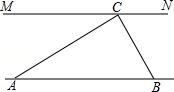
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,所有正方形的中心均在坐标原点,且各边与x轴或y轴平行,从内到外,它们的边长依次为2,4,6,8 …,顶点依次为A1,A2,A3,A4,A5,…,则顶点A55的坐标是( )

A. (13,13) B. (-13,-13) C. (-14,-14) D. (14,14)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,隧道的截面由半圆和长方形构成,长方形的长BC为8m,宽AB为1m,该隧道内设双向行驶的车道(共有2条车道),若现有一辆货运卡车高4m,宽2.3m。则这辆货运卡车能否通过该隧道?说明理由.
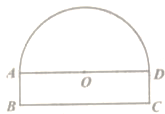
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线
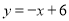 与x和y轴分别交于点B和点C,与直线OA相交于点A(4,2),动点M在线段OA和射线AC上运动.
与x和y轴分别交于点B和点C,与直线OA相交于点A(4,2),动点M在线段OA和射线AC上运动.(1)求点B和点C的坐标.
(2)求△OAC的面积.
(3)是否存在点M,使△OMC的面积是△OAC的面积的
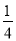 ?若存在,求出此时点M的坐标,若不存在,说明理由.
?若存在,求出此时点M的坐标,若不存在,说明理由.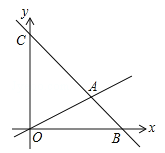
相关试题

