【题目】某水果专卖店销售樱桃,其进价为每千克![]() 元,按每千克
元,按每千克![]() 元出售,平均每天可售出
元出售,平均每天可售出![]() 千克,后来经过市场调查发现,单价每千克降低
千克,后来经过市场调查发现,单价每千克降低![]() 元,则平均每天的销售可增加
元,则平均每天的销售可增加![]() 千克,若该专卖店销售这种樱桃要想平均每天获利
千克,若该专卖店销售这种樱桃要想平均每天获利![]() 元,请回答:
元,请回答:
(![]() )每千克樱桃应降价多少元?
)每千克樱桃应降价多少元?
(![]() )在平均每天获利不变的情况下,为尽可能让利于顾客,赢得市场,该店应按原售价的几折出售?
)在平均每天获利不变的情况下,为尽可能让利于顾客,赢得市场,该店应按原售价的几折出售?
参考答案:
【答案】(1)4元或6元.(2)九折.
【解析】试题分析:(1)设每千克水果应降价x元,利用销售量×每件利润=2240元列出方程求解即可;
(2)为了让利于顾客因此应下降6元,求出此时的销售单价即可确定几折.
试题解析:
(![]() )设每千克水果应降价
)设每千克水果应降价![]() 元,
元,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
, ![]() ,
,
答:每千克樱桃应降价![]() 元或
元或![]() 元.
元.
(![]() )∵尽可能让利于顾客,
)∵尽可能让利于顾客,
∴应降价![]() 元,
元,
则售价为![]() 元,
元,
![]() ,
,
答:该店应按原价的九折出售.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线
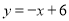 与x和y轴分别交于点B和点C,与直线OA相交于点A(4,2),动点M在线段OA和射线AC上运动.
与x和y轴分别交于点B和点C,与直线OA相交于点A(4,2),动点M在线段OA和射线AC上运动.(1)求点B和点C的坐标.
(2)求△OAC的面积.
(3)是否存在点M,使△OMC的面积是△OAC的面积的
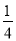 ?若存在,求出此时点M的坐标,若不存在,说明理由.
?若存在,求出此时点M的坐标,若不存在,说明理由.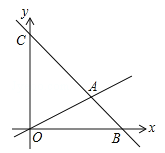
-
科目: 来源: 题型:
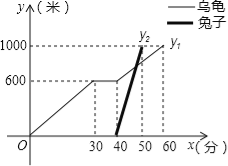
查看答案和解析>>【题目】“龟兔首次赛跑”之后,输了比赛的兔子没有气馁,总结反思后,和乌龟约定再赛一场.图中的函数图象刻画了“龟兔再次赛跑”的故事(x表示乌龟从起点出发所行的时间,y1表示乌龟所行的路程,y2表示兔子所行的路程).有下列说法:
①“龟兔再次赛跑”的路程为1000米;
②兔子和乌龟同时从起点出发;
③乌龟在途中休息了10分钟;
④兔子在途中750米处追上乌龟.
其中正确的说法是 .(把你认为正确说法的序号都填上)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某小区为了绿化环境,计划分两次购进A、B两种花草,第一次分别购进A、B两种花草30棵和15棵,共花费675元;第二次分别购进A、B两种花草12棵和5棵.两次共花费940元(两次购进的A、B两种花草价格均分别相同).
(1)A、B两种花草每棵的价格分别是多少元?
(2)若购买A、B两种花草共31棵,且B种花草的数量少于A种花草的数量的2倍,请你给出一种费用最省的方案,并求出该方案所需费用. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),…,按这样的运动规律,经过第2011次运动后,动点P的坐标是____________。

-
科目: 来源: 题型:
查看答案和解析>>【题目】销售有限公司到某汽车制造有限公司选购A、B两种型号的轿车,用300万元可购进A型轿车10辆,B型轿车15辆;用300万元可购进A型轿车8辆,B型轿车18辆.
(1)求A、B两种型号的轿车每辆分别多少元?
(2)若该汽车销售公司销售一辆A型轿车可获利8000元,销售一辆B型轿车可获利5000元,该汽车销售公司准备用不超过400万元购进A、B两种型号轿车共30辆,且这两种轿车全部售出后总获利不低于20.4万元,问:有几种购车方案?在这几种购车方案中,哪种获利最多?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,矩形OEFG的顶点E的坐标为(4,0),顶点G的坐标为(0,2),将矩形OEFG绕点O逆时针旋转,使点F落在y轴的点N处,得到矩形OMNP,OM与GF交于点A.
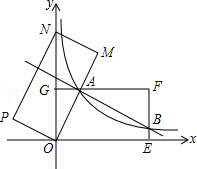
(1)求图象经过点A的反比例函数的解析式;
(2)设(2)中的反比例函数图象交EF于点B,直接写出直线AB的解析式.
相关试题

