【题目】如图,在长方形ABCD中,AD=BC,AB=CD,AD>AB,将长方形ABCD折叠,使点C与点A重合,折痕为MN,连接CN.若△CDN的面积与△CMN的面积比为1:3,
(1)求证:DN=BM;(2)求ND:NA的值;(3)求MN2:BM2的值.

参考答案:
【答案】(1)见解析;(2)1:3;(3)12
【解析】
(1)利用证明全等三角形得出DN=BM;(2)利用面积之比推出三角形对应边之比;(3)过点N作NG⊥BC于G,推出CDNG为矩形,根据矩形的性质推出边之比,设DN=x,用x表示MN及BM,即可得出答案.
(1)∵∠EAN=90°,∠BAN=90°且∠NAE为公共角.
∴∠EAN=∠BAM.又∵AB=CD,∠B=∠D=90°
∴△ABM≌△CDN(ASA)
∴DN=BM
(2)∵ △CDN的面积与△CMN的面积比为1:3,他们等高.
∴DN:MC=1:3
又∵AN∥CM,AM∥CN
∴四边形AMCN为平行四边形,且由于折叠时CM=AM
∴四边形AMCN为菱形.
∴DN:MC=DN:NA=1:3
(3)过点N作NG⊥BC于G,如图.

∵四边形ABCD是矩形,
∴四边形CDNG是矩形,AD∥BC,∴CD=NG,CG=DN,
∠ANM=∠CMN,由折叠的性质可得:AM=CM,∠AMN=∠CMN,
∴∠ANM=∠AMN
∴AM=AN,
∴四边形AMCN是平行四边形,
∵AM=CM,
∴四边形AMCN是菱形,
∵△CDN的面积与△CMN的面积比为1:3,
∴DN:CM=1:3,
设DN=x,
则AM=AN=CM=CN=3x,AD=BC=4x,CG=x,
∴BM=x,GM=2x,
在Rt△CGN中,NG=![]() =
=![]() =2
=2![]()
![]() .
.
在Rt△MNG中,MN=![]() =
=![]() =2
=2![]() x
x
∴![]() =
=![]() =12..
=12..
故答案为:12.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:点C在直线AB上,AC=8cm,BC=6cm,点M、N分别是AC、BC的中点,求线段MN的长.
-
科目: 来源: 题型:
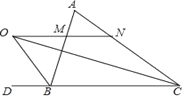
查看答案和解析>>【题目】如图,已知在△ABC中,△ABC的外角∠ABD的平分线与∠ACB的平分线交于点O,MN过点O,且MN∥BC,分别交AB、AC于点M、N.
求证:(1)MO=MB;(2)MN=CN﹣BM.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,阴影部分是边长为a的大正方形中剪去一个边长为b的小正方形后所得到的图形,将阴影部分通过割、拼,形成新的图形,给出下列3种割拼方法,其中能够验证平方差公式的是( )

A. ①② B. ②③ C. ①③ D. ①②③
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系中,平行四边形OABC的顶点C(3,4),边OA落在x正半轴上,P为线段AC上一点,过点P分别作DE∥OC,FG∥OA交平行四边形各边如图.若反比例函数
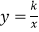 的图象经过点D,四边形BCFG的面积为8,则k的值为( )
的图象经过点D,四边形BCFG的面积为8,则k的值为( ) 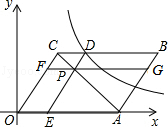
A.16
B.20
C.24
D.28 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把Rt△ABC放在直角坐标系内,其中∠CAB=90°,BC=5,点A、B的坐标分别为(1,0)、(4,0),将△ABC沿x轴向右平移,当点C落在直线y=2x﹣6上时,线段BC扫过的面积为 cm2 .
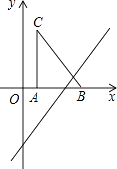
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:
(1)a2b-abc; (2)3a(x-y)+9(y-x);
(3)(2a-b)2+8ab; (4)(m2-m)2+
 (m2-m)+
(m2-m)+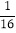 .
.
相关试题

