搜索
【题目】如图，平面直角坐标系中，平行四边形OABC的顶点C（3，4），边OA落在x正半轴上，P为线段AC上一点，过点P分别作DE∥OC，FG∥OA交平行四边形各边如图．若反比例函数 
的图象经过点D，四边形BCFG的面积为8，则k的值为（ ）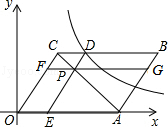 
A.16
B.20
C.24
D.28
参考答案：
【答案】B
【解析】解：由图可得， 
SABCD ， 又∵S△FCP=S△DCP且S△AEP=S△AGP ，
∴SOEPF=SBGPD ，
∵四边形BCFG的面积为8，
∴SCDEO=SBCFG=8，
又∵点C的纵坐标是4，则CDOE的高是4，
∴OE=CD= 
，
∴点D的横坐标是5，
即点D的坐标是（5，4），
∴4= 
，解得k=20，
故选B．
根据图形可得，△CPF与△CPD的面积相等，△APE与△APG的面积相等，四边形BCFG的面积为8，点C（3，4），可以求得点D的坐标，从而可以求得k的值．
-
科目： 来源： 题型：
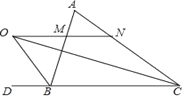
查看答案和解析>>【题目】如图，已知在△ABC中，△ABC的外角∠ABD的平分线与∠ACB的平分线交于点O，MN过点O，且MN∥BC，分别交AB、AC于点M、N．
求证：（1）MO=MB；（2）MN=CN﹣BM．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，阴影部分是边长为a的大正方形中剪去一个边长为b的小正方形后所得到的图形，将阴影部分通过割、拼，形成新的图形，给出下列3种割拼方法，其中能够验证平方差公式的是( )
A. ①② B. ②③ C. ①③ D. ①②③
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在长方形ABCD中，AD=BC,AB=CD,AD＞AB，将长方形ABCD折叠，使点C与点A重合，折痕为MN，连接CN．若△CDN的面积与△CMN的面积比为1：3，
（1）求证：DN=BM；（2）求ND:NA的值；（3）求MN2：BM2的值.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，把Rt△ABC放在直角坐标系内，其中∠CAB=90°，BC=5，点A、B的坐标分别为（1，0）、（4，0），将△ABC沿x轴向右平移，当点C落在直线y=2x﹣6上时，线段BC扫过的面积为 cm2 ．
-
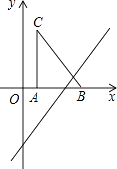
科目： 来源： 题型：
查看答案和解析>>【题目】分解因式：
(1)a2b－abc； (2)3a(x－y)＋9(y－x)；
(3)(2a－b)2＋8ab； (4)(m2－m)2＋
(m2－m)＋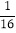
. -
科目： 来源： 题型：
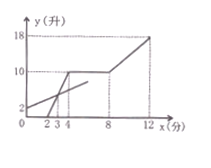
查看答案和解析>>【题目】现有甲、乙两个容器，分别装有进水管和出水管 ，两容器的进出水速度不变，先打开乙容器的进水管，2分钟时再打开甲容器的进水管，又过2分钟关闭甲容器的进水管，再过4分钟同时打开甲容器的进、出水管。直到12分钟时，同时关闭两容器的进出水管。打开和关闭水管的时间忽略不计。容器中的水量y(升)与乙容器注水时间x(分)之间的关系如图所示
（1）求甲容器的进、出水速度；
（2）当
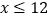时，在这过程中是否存在两容器的水量相等？若存在，求出此时x的值； （3）如果在乙容器中再装一个进水管，其进水速度是2升／分，若使两容器第12分钟时的水量相等 ，则应该在第几分钟打开此进水管？
相关试题
