【题目】已知,如图1, ![]() 分别为定角(大小不会发生改变)
分别为定角(大小不会发生改变) ![]() 内部的两条动射线,
内部的两条动射线,![]() 与
与 ![]() 互补,
互补,![]() .
.

(1)求![]() 的度数:
的度数:
(2)如图2,射线![]() 分别为
分别为![]() 的平分线,当
的平分线,当![]() 绕着点
绕着点![]() 旋转时,下列结论:①
旋转时,下列结论:①![]() 的度数不变:②
的度数不变:②![]() 的度数不变,其中只有一个是正确的,请你做出正确的选择并求值:
的度数不变,其中只有一个是正确的,请你做出正确的选择并求值:
(3)如图3, ![]() 是
是![]() 外部的两条射线,且
外部的两条射线,且![]() ,
, ![]()
![]() ,当
,当![]() 绕着点
绕着点![]() 旋转时,
旋转时,![]() 的大小是否会发生变化?若不变,求出其度数:若变化,说明理由,
的大小是否会发生变化?若不变,求出其度数:若变化,说明理由,
参考答案:
【答案】(1)![]() ;(2)②正确,
;(2)②正确,![]() 的度数为90°不变;(3)
的度数为90°不变;(3) ![]() 的大小不变为130° ,
的大小不变为130° ,
【解析】
(1)根据角的定义可知∠AOC+∠BOD=180°,与∠AOB+∠COD=50°,结合可得∠BOC的度数,即可求出∠AOD的度数;
(2)根据角平分线的定义得出∠MON=∠CON+∠BOM+∠BOC=25°+65°=90°;
(3)先求得∠DOE+∠AOF的值,再根据角平分线的定义得出∠POD+∠AOQ,再加上∠AOD即可得∠POQ的值.
解: (1)∵![]() 互补,
互补,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ;
;
(2)②正确,![]() 的度数为90°不变;理由如下: .
的度数为90°不变;理由如下: .
∵![]() 的平分线,
的平分线,
∴![]() ,
,
∴![]() ,
,
故②正确,![]() 的度数为90°不变;
的度数为90°不变;
(3) ![]() 的大小不变为130° ,
的大小不变为130° ,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A,B两点在数轴上对应的数分别为a,b,且点A在点B的左边,|a|=10,a+b=80,ab<0.
(1)求出a,b的值;
(2)现有一只电子蚂蚁P从点A出发,以3个单位长度/秒的速度向右运动,同时另一只电子蚂蚁Q从点B出发,以2个单位长度/秒的速度向左运动.
①设两只电子蚂蚁在数轴上的点C相遇,求出点C对应的数是多少?
②经过多长时间两只电子蚂蚁在数轴上相距20个单位长度?

-
科目: 来源: 题型:
查看答案和解析>>【题目】在2016年泉州市初中体育中考中,随意抽取某校5位同学一分钟跳绳的次数分别为:158,160,154,158,170,则由这组数据得到的结论错误的是( )
A. 平均数为160 B. 中位数为158 C. 众数为158 D. 方差为20.3
-
科目: 来源: 题型:
查看答案和解析>>【题目】李老师家距学校1900米,某天他步行去上班,走到路程的一半时发现忘带手机,此时离上班时间还有23分钟,于是他立刻步行回家取手机,随后骑电瓶车返回学校.已知李老师骑电瓶车到学校比他步行到学校少用20分钟,且骑电瓶车的平均速度是步行速度的5倍,李老师到家开门、取手机、启动电瓶车等共用4分钟.
(1)求李老师步行的平均速度;
(2)请你判断李老师能否按时上班,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解我市3路公共汽车的运营情况,公交部门随机统计了某天3路公共汽车50个班次中每个运行班次的载客量,得到如下频数分布直方图,如果以各组的组中值代表各组实际数据,请分析统计数据完成下列问题:
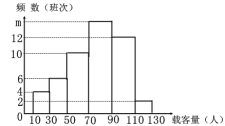
(1)直方图中m值为________;
(2)这天载客量的中位数是__________,众数是__________;
(3)估计往常3路公共汽车平均每班次的载客量大约是多少(精确到整数)?
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两车分别从相距240千米的A,B两地同时相向匀速出发,甲车出发0.5小时后发现有东西落在出发地A地,于是立即按原速沿原路返回,在A地取到东西后立即以原速继续向B地行驶,并在途中与乙车第一次相遇,相遇后甲、乙两车继续以各自的速度朝着各自的方向匀速行驶,当乙车到达A地后,立即掉头以原速开往B地(甲车取东西、掉头和乙车掉头的时间均忽略不计).两车之间的距离y(千米)与甲车出发的时间x(小时)之间的部分关系如图所示,则当乙车到达B地时,甲车与B地的距离为_____千米.
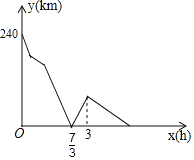
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点A的坐标是(0,3),点B的坐标是(-4,0).
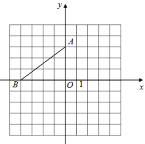
(1)画出△AOB绕点A逆时针旋转90°后得到的图形△A1O1B1;并写出点B1的坐标 ;
(2)画出△AOB关于点P(0,-1)的中心对称图形△A2O2B2,并写出点B2的坐标 ;
(3)若点Q为x轴上的一点,当B1Q+B2 Q的和最小时,直接写出点Q的坐标.
相关试题

