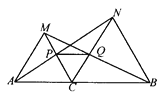
【题目】已知:如图,点C在线段AB上,以AC和BC为边在AB的同侧作正三角形△ACM和△BCN,连结AN、BM,分别交CM、CN于点P、Q.求证:PQ∥AB.
参考答案:
【答案】见解析
【解析】试题分析:首先证明△ACN≌△MCB可得∠ANC=∠MBC,再证明△PCN≌△QCB可得PC=QC,再有∠MCN=60°可得△PCQ是等边三角形,进而得到∠PQC=60°,可证明PQ∥AB.
试题解析:∵△ACM和△BCN都是正三角形,
∴∠ACM=∠BCN=60°,AC=CM,BC=CN.
∵点C在线段AB上,
∴∠ACM=∠BCN=∠MCN=60°.
∴∠ACM+∠MCN=∠BCN+∠MCN=120°.
即∠NCA=∠BCM=120°.
∵在△ACN和△MCB中,
 ,
,
∴△ACN≌△MCB(SAS),
∴∠ANC=∠MBC,
∵在△PCN和△QCB中,
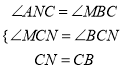 ,
,
∴△PCN≌△QCB(AAS),
∴PC=QC,
∵∠PCQ=60°,
∴△PCQ是等边三角形,
∴∠PQC=60°,
∴∠PQC=∠QCB,
∴PQ∥AB.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB=AD,添加下列一个条件后,仍无法确定△ABC≌△ADC的是( )
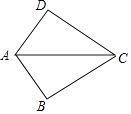
A.BC=CD
B.∠BAC=∠DAC
C.∠B=∠D=90°
D.∠ACB=∠ACD -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在△ABC中有D、E两点,求证:BD+DE+EC<AB+AC.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在一次体育测试中,小芳所在小组8个人的成绩分别是:46,47,48,48,49,49,49,50.则这8个人体育成绩的中位数是( )
A.47B.48C.48.5D.49
-
科目: 来源: 题型:
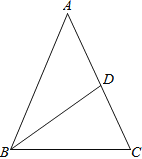
查看答案和解析>>【题目】如图,已知△ABC中,AB=AC,周长为24,AC边上的中线BD把△ABC分成周长差为6的两个三角形,则△ABC各边的长分别为多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,已知AC是矩形纸片ABCD的对角线,AB =3,BC =4.现将矩形ABCD沿对角线AC剪开,再把△ABC沿着AD方向平移,得到图②中△A′BC′,当四边形A′ECF是菱形时,平移距离AA′的长是___________.
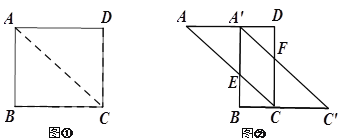
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一个有理数与它的相反数的差为一个负数,则( )
A.这个有理数一定是负数
B.这个有理数一定是正数
C.这个有理数可为正数,也可为负数
D.这个有理数一定是零
相关试题

