【题目】已知:如图,在△ABC中有D、E两点,求证:BD+DE+EC<AB+AC.

参考答案:
【答案】见解析
【解析】试题分析:延长BD交AC于M点,延长CE交BD的延长线于点N.在△ABM中,AB+AM>BM,在△CNM中,NM+MC>NC,所以AB+AM+NM+MC>BM+NC,再由AM+MC=AC,BM=BN+NM可知AB+AC+NM>BN+NM+NC,故AB+AC>BN+NC,在△BNC中,BN+NC=BD+DN+NE+EC,在△DNE中,DN+NE>DE,由此即可得出结论.
试题解析:延长BD交AC于M点,延长CE交BD的延长线于点N.
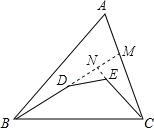
在△ABM中,AB+AM>BM,
在△CNM中,NM+MC>NC,
∴AB+AM+NM+MC>BM+NC,
∵AM+MC=AC,BM=BN+NM,
∴AB+AC+NM>BN+NM+NC,
∴AB+AC>BN+NC①
在△BNC中,BN+NC=BD+DN+NE+EC,②
在△DNE中,DN+NE>DE③
由②、③得:BN+NC>BD+DE+EC④
由①、④得:AB+AC>BN+NC>BD+DE+EC.
即:BD+DE+EC<AB+AC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】点 A 的坐标(﹣3,4),它到 y 轴的距离为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个正数的两个平方根分别是 3-x 和 2x+6 ,则 x 的值是______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB=AD,添加下列一个条件后,仍无法确定△ABC≌△ADC的是( )
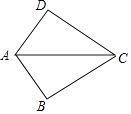
A.BC=CD
B.∠BAC=∠DAC
C.∠B=∠D=90°
D.∠ACB=∠ACD -
科目: 来源: 题型:
查看答案和解析>>【题目】在一次体育测试中,小芳所在小组8个人的成绩分别是:46,47,48,48,49,49,49,50.则这8个人体育成绩的中位数是( )
A.47B.48C.48.5D.49
-
科目: 来源: 题型:
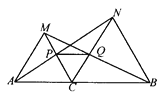
查看答案和解析>>【题目】已知:如图,点C在线段AB上,以AC和BC为边在AB的同侧作正三角形△ACM和△BCN,连结AN、BM,分别交CM、CN于点P、Q.求证:PQ∥AB.
-
科目: 来源: 题型:
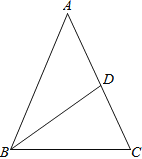
查看答案和解析>>【题目】如图,已知△ABC中,AB=AC,周长为24,AC边上的中线BD把△ABC分成周长差为6的两个三角形,则△ABC各边的长分别为多少?
相关试题

