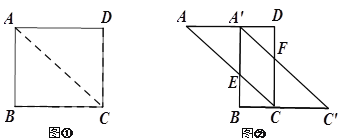
【题目】如图①,已知AC是矩形纸片ABCD的对角线,AB =3,BC =4.现将矩形ABCD沿对角线AC剪开,再把△ABC沿着AD方向平移,得到图②中△A′BC′,当四边形A′ECF是菱形时,平移距离AA′的长是___________.
参考答案:
【答案】2.5
【解析】由矩形的性质求得AC=5,由平移的性质求得A/B=DC=3,设AA/=x,则A/D=4-x,由菱形的性质得出A/E∥FC,A/E=EC,由平行线的性质得出△AA/E∽△ADC,由相似的性质得出![]() =
=![]() =
=![]() ,求出AE=
,求出AE=![]() x,A′E=
x,A′E=![]() x,EC=AC-AE=5-
x,EC=AC-AE=5-![]() x,得出
x,得出![]() x=5-
x=5-![]() x,求出x即可得出结果.
x,求出x即可得出结果.
解:∵矩形纸片ABCD,AB =3,BC =4
∴在图②中,AD=4,A′B=DC=3,AC=![]() ,
,
设A A′=x,∴A′D=4-x,
∵四边形A′ECF是菱形,
∴A/E∥FC,A/E=EC,
∴△AA/E∽△ADC,由相似的性质得出![]() =
=![]() =
=![]() ,
,
AE=![]() x,A′E=
x,A′E=![]() x,EC=AC-AE=5-
x,EC=AC-AE=5-![]() x,
x,
∴![]() x=5-
x=5-![]() x,
x,
解得:x=2.5.
故答案为:2.5.
“点睛”本题考查了矩形的性质、勾股定理、平移的性质、菱形的性质三角形相似的判定与性质等知识;熟练掌握三角形相似的判定与性质是解决问题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一次体育测试中,小芳所在小组8个人的成绩分别是:46,47,48,48,49,49,49,50.则这8个人体育成绩的中位数是( )
A.47B.48C.48.5D.49
-
科目: 来源: 题型:
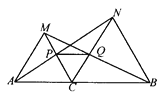
查看答案和解析>>【题目】已知:如图,点C在线段AB上,以AC和BC为边在AB的同侧作正三角形△ACM和△BCN,连结AN、BM,分别交CM、CN于点P、Q.求证:PQ∥AB.
-
科目: 来源: 题型:
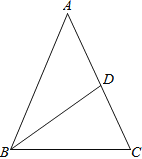
查看答案和解析>>【题目】如图,已知△ABC中,AB=AC,周长为24,AC边上的中线BD把△ABC分成周长差为6的两个三角形,则△ABC各边的长分别为多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一个有理数与它的相反数的差为一个负数,则( )
A.这个有理数一定是负数
B.这个有理数一定是正数
C.这个有理数可为正数,也可为负数
D.这个有理数一定是零
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在△ABC中,AB=AC。

(1)若D为AC的中点,BD把三角形的周长分为24cm和30cm两部分,求△ABC三边的长;
(2)若D为AC上一点,试说明AC>
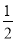 (BD+DC)。
(BD+DC)。 -
科目: 来源: 题型:
查看答案和解析>>【题目】(本题满分8分)我们知道当人的视线与物体表面互相垂直时的视觉效果最佳.如图是小明站在距离墙壁1.60米处观察装饰画时的示意图,此时小明的眼睛与装饰画底部A处于同一水平线上,视线恰好落在装饰画中心位置E处,且与AD垂直.已知装饰画的高度AD为0.66米,
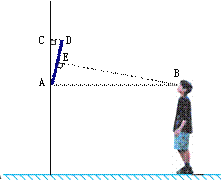
求:⑴ 装饰画与墙壁的夹角∠CAD的度数(精确到1°);
⑵ 装饰画顶部到墙壁的距离DC(精确到0.01米).
相关试题

