搜索
【题目】已知多项式
的常数项是a，次数是b，且a，b两个数轴上所对应的点分别为A、B，若点A、点B同时沿数轴向正方向运动，点A的速度是点B的2倍，且3秒后，
，求点B的速度为（ ）
A.
B.
或 C.或
D.
参考答案：
【答案】C
【解析】
根据多项式中常数项及多项式的次数的定义求出a和b，设点B的速度为v，则A的速度为2v，分A在原点O的左边与A在原点O的右边进行讨论即可.
解：∵多项式x3-3xy2-4的常数项是a，次数是b，
∴a=-4，b=3，
设B速度为v，则A的速度为2v，3秒后点A在数轴上表示的数为（-4+6v），B点在数轴上表示的数为3+3v，且OB=3+3v
当A还在原点O的左边时，OA=0-（-4+6v）=4-6v，由
可得
，解得
；
当A还在原点O的右边时，OA=（-4+6v）-0=6v-4，由可得
，解得
.
故B的速度为
或
，选C.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在Rt△ABC中，∠C=90°，以AC为直径作⊙O，交AB于D，过点O作OE∥AB，交BC于E．
（1）求证：ED为⊙O的切线；
（2）如果⊙O的半径为
，ED=2，延长EO交⊙O于F，连接DF、AF，求△ADF的面积．
【答案】（1）证明见解析；（2）
【解析】试题分析：（1）首先连接OD，由OE∥AB，根据平行线与等腰三角形的性质，易证得
≌
即可得
，则可证得
为
的切线；
（2）连接CD，根据直径所对的圆周角是直角，即可得
利用勾股定理即可求得
的长，又由OE∥AB，证得
根据相似三角形的对应边成比例，即可求得
的长，然后利用三角函数的知识，求得
与
的长，然后利用S△ADF=S梯形ABEF-S梯形DBEF求得答案．试题解析：(1)证明：连接OD，
∵OE∥AB，
∴∠COE=∠CAD，∠EOD=∠ODA，
∵OA=OD,
∴∠OAD=∠ODA，
∴∠COE=∠DOE，
在△COE和△DOE中，
∴△COE≌△DOE(SAS)，
∴ED⊥OD，
∴ED是
的切线；(2)连接CD，交OE于M，
在Rt△ODE中，
∵OD=32，DE=2，
∵OE∥AB，
∴△COE∽△CAB，
∴AB=5，∵AC是直径，
∵EF∥AB，
∴S△ADF=S梯形ABEFS梯形DBEF
∴△ADF的面积为
【题型】解答题
【结束】
25【题目】【题目】已知，抛物线y=ax2+ax+b（a≠0）与直线y=2x+m有一个公共点M（1，0），且a＜b．
（1）求b与a的关系式和抛物线的顶点D坐标（用a的代数式表示）；
（2）直线与抛物线的另外一个交点记为N，求△DMN的面积与a的关系式；
（3）a=﹣1时，直线y=﹣2x与抛物线在第二象限交于点G，点G、H关于原点对称，现将线段GH沿y轴向上平移t个单位（t＞0），若线段GH与抛物线有两个不同的公共点，试求t的取值范围．
-
科目： 来源： 题型：
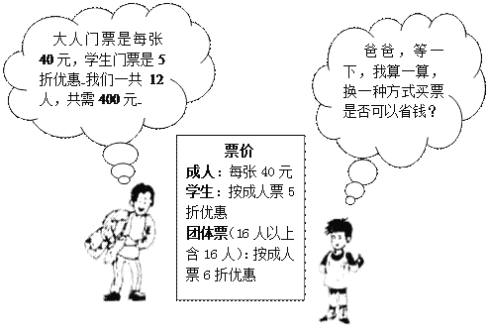
查看答案和解析>>【题目】暑假期间，七（2）班的张明、王强等同学随家长一同到某公园游玩，下面是购买门票时，张明与他爸爸的对话（如图），试根据图中的信息，解答下列问题：
⑴ 张明他们一共去了几个成人，几个学生？
⑵ 请你帮助张明算一算，用哪种方式购票(团体购票还是非团体购票)更省钱？
说明理由．
⑶ 正要购票时，张明发现七（3）班的张小毛等15名同学和他们的2名家长共17人也来购票，请你为他们设计出最省的购票方案，并求出此时的购票费用.
-
科目： 来源： 题型：
查看答案和解析>>【题目】有理数数a，b在轴上的表示如图所示，则下列结论中：①ab＜0，②a+b＜0，③a﹣b＜0，④a＜
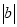，⑤﹣a＞﹣b，正确的有（ ）
A.2个B.3个C.4个D.5个
-
科目： 来源： 题型：
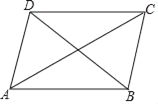
查看答案和解析>>【题目】如图，在四边形ABCD中，对角线AC平分∠DAB，∠ABD=52°，∠ABC=116°，∠ACB=α°，则∠BDC的度数为（ ）
A. α B.
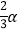C. 90﹣α D. 90﹣ -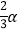
科目： 来源： 题型：
查看答案和解析>>【题目】计算题
（1）（+19）+（﹣27）﹣（+10）﹣23+（﹣49）
（2）（
）×（﹣30）（3）
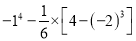
（4）
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，OM是∠AOC的平分线.ON是∠BOC的平分线.
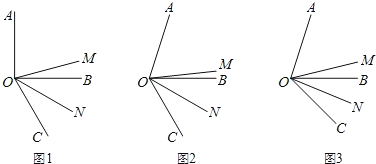
（1）如图1，当∠AOB=90°，∠BOC=60°时，∠MON的度数是多少？为什么？
（2）如图2，当∠AOB=70°，∠BOC=60°时，∠MON= （直接写出结果）
（3）如图3，当∠AOB=α，∠BOC=β时，猜想：∠MON﹣∠CON= （直接写出结果）
相关试题
