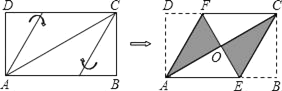
【题目】将矩形纸片ABCD按如图所示的方式折叠,恰好得到菱形AECF.若AB=3,则菱形AECF的面积为_____.
参考答案:
【答案】![]()
【解析】
根据菱形AECF,得∠FCO=∠ECO,再利用∠ECO=∠ECB,可通过折叠的性质,结合直角三角形勾股定理求得BC的长,则利用菱形的面积公式即可求解.
解:∵四边形AECF是菱形,AB=3,
∴设BE=x,则AE=3﹣x,CE=3﹣x,
∵四边形AECF是菱形,
∴∠FCO=∠ECO,
∵∠ECO=∠ECB,
∴∠ECO=∠ECB=∠FCO=30°,
∴2BE=CE,
∴CE=2x,
∴2x=3﹣x,
解得:x=1,
∴CE=2,利用勾股定理得出:
BC2+BE2=EC2,
BC=![]()
又∵AE=AB﹣BE=3﹣1=2,
则菱形的面积=AEBC=![]() .
.
故答案为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(11分)如图,抛物线y=ax2+bx﹣3与x轴交于A,B两点,与y轴交于C点,且经过点(2,﹣3a),对称轴是直线x=1,顶点是M.
(1)求抛物线对应的函数表达式;
(2)经过C,M两点作直线与x轴交于点N,在抛物线上是否存在这样的点P,使以点P,A,C,N为顶点的四边形为平行四边形?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)设直线y=﹣x+3与y轴的交点是D,在线段BD上任取一点E(不与B,D重合),经过A,B,E三点的圆交直线BC于点F,试判断△AEF的形状,并说明理由;
(4)当E是直线y=﹣x+3上任意一点时,(3)中的结论是否成立(请直接写出结论).

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知C,D为线段AB上的两点,点M,N分别为AC与BD的中点,若AB=13,CD=5,求线段MN的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一辆最大载重48吨的大型货车,货车的货箱是长14m,宽2.5m,高3m的长方体,现有甲种货物18吨,乙种货物70m3,而甲种货物每吨的体积为2.5m3,乙种货物每立方米0.5吨.问:
(1)甲、乙两种货物是否都能装上车?请说明理由.
(2)为了最大地利用车的载重量和货箱的容积,两种货物应各装多少吨?
-
科目: 来源: 题型:
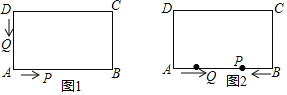
查看答案和解析>>【题目】如图1,在长方形ABCD中,AB=12厘米,BC=6厘米,点P沿AB边从点A开始向点B以2厘米/秒的速度移动;点Q沿DA边从点D开始向点A以1厘米/秒的速度移动.如果P、Q同时出发,用t(秒)表示移动的时间,那么:
(1)如图1,当点P到达点B,或点Q到达点A时,两点都停止运动.
①当t=3时,分别求AQ和BP的长;
②当t为何值时,线段AQ与线段AP相等?
(2)如图2,若P,Q到达B,A后速度不变继续运动,点Q开始向点B移动,P点返回向点A移动,其中一点到达目标点后就停止运动.问当t为何值时,线段PQ的长度等于线段BC长度的一半.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在△ABC中,D、E分别是AB、BC边上的中点,过点C作CF∥AB,交DE的延长线于F点,连接CD、BF.
(1)求证:△BDE≌△CFE;
(2)△ABC满足什么条件时,四边形BDCF是矩形?

-
科目: 来源: 题型:
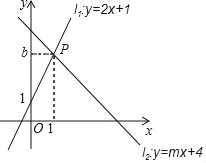
查看答案和解析>>【题目】如图,直线l1:y=2x+1与直线l2:y=mx+4相交于点P(1,b).
(1)求b,m的值;
(2)垂直于x轴的直线与直线l1,l2,分别交于点C,D,垂足为点E,设点E的坐标为(a,0)若线段CD长为2,求a的值.
相关试题

