【题目】已知:如图,在△ABC中,D、E分别是AB、BC边上的中点,过点C作CF∥AB,交DE的延长线于F点,连接CD、BF.
(1)求证:△BDE≌△CFE;
(2)△ABC满足什么条件时,四边形BDCF是矩形?

参考答案:
【答案】(1)详见解析;(2)当BC=AC时,四边形BDCF是矩形,理由详见解析
【解析】
(1)由平行线的性质得出∠DBE=∠CFE,由中点的定义得出BE=CE,由ASA证明△BDE≌△CFE即可;
(2)先证明DE是△ABC的中位线,得出DE∥AC,证出四边形BDCF是平行四边形,得出AD=CF,证出CF=BD,得出四边形BDCF是平行四边形;再由等腰三角形的性质得出CD⊥AB,即可得出结论.
(1)证明:∵CF∥AB,
∴∠DBE=∠CFE,
∵E是BC的中点,
∴BE=CE,
在△BDE和△CFE中,
∴△BDE≌△CFE(ASA);
(2)解:当BC=AC时,四边形BDCF是矩形,理由如下:
∵D、E分别是AB,BC的中点
∴DE是△ABC的中位线,
∴DE∥AC,又AF∥BC,
∴四边形BDCF是平行四边形,
∴AD=CF,
又BD=AD,
∴CF=BD,又CF∥BD,
∴四边形BDCF是平行四边形;
∵BC=AC,BD=AD,
∴CD⊥AB,即∠BDC=90°,
∴平行四边形BDCF是矩形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】一辆最大载重48吨的大型货车,货车的货箱是长14m,宽2.5m,高3m的长方体,现有甲种货物18吨,乙种货物70m3,而甲种货物每吨的体积为2.5m3,乙种货物每立方米0.5吨.问:
(1)甲、乙两种货物是否都能装上车?请说明理由.
(2)为了最大地利用车的载重量和货箱的容积,两种货物应各装多少吨?
-
科目: 来源: 题型:
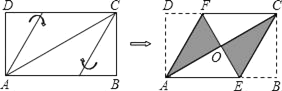
查看答案和解析>>【题目】将矩形纸片ABCD按如图所示的方式折叠,恰好得到菱形AECF.若AB=3,则菱形AECF的面积为_____.
-
科目: 来源: 题型:
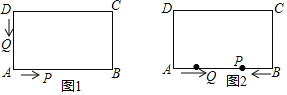
查看答案和解析>>【题目】如图1,在长方形ABCD中,AB=12厘米,BC=6厘米,点P沿AB边从点A开始向点B以2厘米/秒的速度移动;点Q沿DA边从点D开始向点A以1厘米/秒的速度移动.如果P、Q同时出发,用t(秒)表示移动的时间,那么:
(1)如图1,当点P到达点B,或点Q到达点A时,两点都停止运动.
①当t=3时,分别求AQ和BP的长;
②当t为何值时,线段AQ与线段AP相等?
(2)如图2,若P,Q到达B,A后速度不变继续运动,点Q开始向点B移动,P点返回向点A移动,其中一点到达目标点后就停止运动.问当t为何值时,线段PQ的长度等于线段BC长度的一半.
-
科目: 来源: 题型:
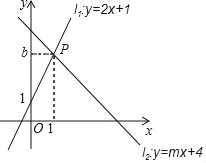
查看答案和解析>>【题目】如图,直线l1:y=2x+1与直线l2:y=mx+4相交于点P(1,b).
(1)求b,m的值;
(2)垂直于x轴的直线与直线l1,l2,分别交于点C,D,垂足为点E,设点E的坐标为(a,0)若线段CD长为2,求a的值.
-
科目: 来源: 题型:
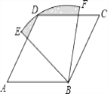
查看答案和解析>>【题目】如图,四边形ABCD是菱形,∠A=60°,AB=6,扇形BEF的半径为6,圆心角为60°,则图中阴影部分的面积是______
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中,点A、B的坐标分别为(1,4)和(3,0),点C是y轴上的一个动点,且A、B、C三点不在同一条直线上,当△ABC的周长最小时,点C的坐标是

A.(0,0)B.(0,1)C.(0,2)D.(0,3)
相关试题

