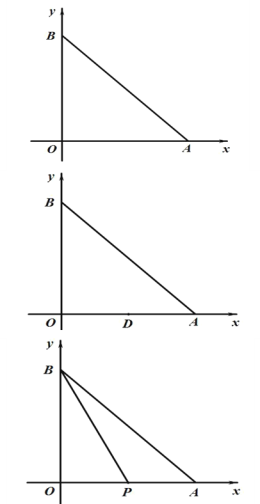
【题目】已知:如图,在平面直角坐标系中,点 A 的坐标为(6,0),AB=6![]() ,点 P 从点 O出发沿线段 OA 向终点 A 运动,点 P 的运动速度是每秒 2 个单位长度,点 D 是线段 OA 的中点.
,点 P 从点 O出发沿线段 OA 向终点 A 运动,点 P 的运动速度是每秒 2 个单位长度,点 D 是线段 OA 的中点.
(1)求点 B 的坐标;
(2)设点 P 的运动时间为点 t 秒,△BDP 的面积为 S,求 S 与 t 的函数关系式;
(3)当点 P 与点 D 重合时,连接 BP,点 E 在线段 AB 上,连接 PE,当∠BPE=2∠OBP 时, 求点 E 的坐标.
参考答案:
【答案】(1)B(0,6);(2)S=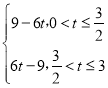 ;(3)E(4,2)
;(3)E(4,2)
【解析】
(1)在Rt△AOB中,利用勾股定理可求得OB的长,从而得到点B的坐标;
(2)存在2种情况,一种是点P在点D的左侧,一种是在右侧,求△PBD的面积,高始终是OB不变,仅需表示出PD的长即可;
(3)如下图,作∠BPE的角平分线PF,根据角之间的关系,可得到PF∥OB,从而推导出△PEG∽△PBO,最后利用相似比的关系求得线段的长度,从而得到E的坐标.
(1)∵A(6,0),AB=6![]() ,△AOB是直角三角形
,△AOB是直角三角形
∴在Rt△AOB中,OB=![]()
∴B(0,6)
(2)情况一:如下图,点P在点D的左侧,即![]() 时
时
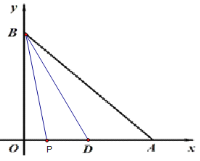
在△BPD中,以PD为底,则BO是△BOD的高
∴高=BO=6,底=3-2t
∴S=![]()
情况二:如下图,点P在点D的右侧,即![]() 时
时
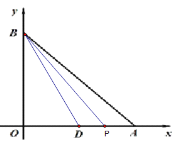
在△BPD中,以PD为底,则BO是△BOD的高
∴高=BO=6,底=2t-3
∴S=![]()
综上得:S=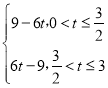
(3)如下图,PF是∠PBE的角平分线,交AB于点F,过点E作x轴的垂线,交x轴于点G
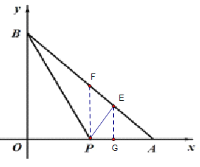
∵OA=6,OB=6,AB=6![]()
∴△OBA是等腰直角三角形,∠A=45°
∴△GEA是等腰直角三角形
设PG=x,则AG=3-x
∴EG=AG=3-x
∵PF是∠BPE的角平分线,∴∠BPF=∠FPE
∵∠BPE=2∠OBP
∴∠OBP=∠BPF=∠FPE
∴PF∥OB,∴PF⊥OA
∴∠FPE+∠EPG=90°
∵∠OBP+∠BPO=90°,∴∠EPG=∠BPO
∵∠EGP=∠BOP
∴△PEG∽△PBO
∴![]() ,即
,即![]() ,解得:x=1
,解得:x=1
∴PG=1,GE=2
∴E(4,2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于
 ,
, 的方程组
的方程组 ,则下列结论中:①当
,则下列结论中:①当 时,方程组的解是
时,方程组的解是 ;②当
;②当 ,
, 的值互为相反数时,
的值互为相反数时, ;③不存在一个实数
;③不存在一个实数 使得
使得 ;④若
;④若 ,则
,则 正确的个数有( )
正确的个数有( )A. 1个B. 2个C. 3个D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:菱形 ABCD,点 E 在线段 BC 上,连接 DE,点 F 在线段 AB 上,连接 CF、DF, CF 与 DE 交于点 G,将菱形 ABCD 沿 DF 翻折,点 A 恰好落在点 G 上.
(1)求证:CD=CF;
(2)设∠CED= x,∠DCF= y,求 y 与 x 的函数关系式;(不要求写出自变量的取值范围)
(3)在(2)的条件下,当 x=45°时,以 CD 为底边作等腰△CDK,顶角顶点 K 在菱形 ABCD的内部,连接 GK,若 GK∥CD,CD=4 时,求线段 KG 的长.


-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知△ABC中,P是边AB上的一点,连接CP.
(1)要使△ACP∽△ABC,还需要补充的一个条件是_____.
(2)若△ACP∽△ABC,且AC=
 ,AB=3,求AP的长.
,AB=3,求AP的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某服装店购进一批甲、乙两种款型时尚T恤衫,甲种款型共用了7800元,乙种款型共用了6400元,甲种款型的件数是乙种款型件数的1.5倍,甲种款型每件的进价比乙种款型每件的进价少30元.
(1)甲、乙两种款型的T恤衫各购进多少件?
(2)商店进价提高60%标价销售,销售一段时间后,甲款型全部售完,乙款型剩余一半,商店决定对乙款型按标价的五折降价销售,很快全部售完,求售完 这批T恤衫商店共获利多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】大家见过形如x+y=z,这样的三元一次方程,并且知道x=3,y=4,z=7就是适合该方程的一个正整数解,法国数学家费尔马早在17世纪还研究过形如x2+y2=z2的方程.
(1)请写出方程x2+y2=z2的两组正整数解: .
(2)研究直角三角形和勾股数时,我国古代数学专著(九章算术)给出了如下数:a=
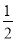 (m2﹣n2),b=mn,c=
(m2﹣n2),b=mn,c=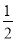 (m2+n2),(其中m>n,m,n是奇数),那么,以a,b,c为三边的三角形为直角三角形,请你加以验证.
(m2+n2),(其中m>n,m,n是奇数),那么,以a,b,c为三边的三角形为直角三角形,请你加以验证. -
科目: 来源: 题型:
查看答案和解析>>【题目】在日常生活中如取款、上网等都需要密码,有一种用“因式分解法”产生的密码,方便记忆,原理是对于多项
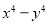 ,因式分解的结果是
,因式分解的结果是 ,若取
,若取 ,
,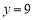 时,则各个因式的值是:
时,则各个因式的值是: ,
, ,
, ,于是就可以把“180162”作为一个六位数的密码,对于多项式
,于是就可以把“180162”作为一个六位数的密码,对于多项式 ,取
,取 ,
, 时,用上述方法产生的密码是________ (写出一个即可).
时,用上述方法产生的密码是________ (写出一个即可).
相关试题

